
L'INVENTION DU BIG BANG
par J.-P. Luminet
Copyright : Editions du Seuil, Paris


par J.-P. Luminet
Copyright : Editions du Seuil, Paris

Ce texte est l'introduction de l'ouvrage A. Friedmann, G. Lemaître :
Essais de Cosmologie, traduction et notes de J.-P. Luminet et A. Grib, Le
Seuil, collections "Sources du Savoir", Paris, 1997.
Pour en voir plus, cliquer ici
Il faut bien que nous vivions, malgré la chute de tant de cieux
D.H.Lawrence, L'amant de Lady Chatterley (1928)
La citation de l'écrivain anglais sonne étrangement juste au regard de deux événements qui se sont déroulés dans le monde occidental entre 1925 et 1935: une crise économique doublée d'une crise cosmologique, aussi brutales qu'imprévisibles - malgré quelques lézardes antérieures dont personne n'avait tenu compte.
Crise économique : en octobre 1929, après une période de prospérité qui semblait durable, la bourse américaine de Wall Street connaît un effondrement spectaculaire. La situation économique et industrielle se dégrade rapidement et la crise gagne l'ensemble des pays industrialisés. Voyant leur univers financier s'effondrer du jour au lendemain, les hommes d'affaires se suicident par dizaines. C'est par millions que se comptent les sans-travail. Près de dix ans seront nécessaires pour redresser la situation sociale.
Sans être aussi dramatique, et n'affectant que le microcosme des physiciens théoriciens et des astronomes de pointe, la crise de la représentation cosmologique qui s'est déroulée simultanément et dans le même intervalle de temps marquera sans doute davantage l'histoire de la pensée humaine que la crise économique. Elle s'est en effet dénouée en ce que l'épistémologue Thomas Kuhn [1].
appelle une révolution scientifique. Il y a révolution scientifique lorsqu'une théorie scientifique consacrée par le temps et l'expérience est rejetée au profit d'une nouvelle théorie. Or, dans le domaine de la cosmologie, la physique n'a connu que trois révolutions scientifiques : la révolution copernico-galiléenne, la révolution newtonienne et la révolution relativiste.
A titre d'exemple, penchons-nous brièvement sur la première d'entre elles. En 1543, Copernic publie De Revolutionibus Orbium Coelestis [2], dans lequel il déplace la Terre du centre du monde au profit du Soleil. En 1572, une étoile nouvelle apparaît dans la constellation de Cassiopée; minutieusement observée par Tycho-Brahé, elle jette le doute sur le dogme aristotélicien de l'immuabilité des étoiles fixes [3]. En 1600, Giordano Bruno est condamné par l'Inquisition après avoir affirmé l'infinité de l'espace, la pluralité de mondes habités et autres hérésies théologiques [4]. En 1609, Johannes Kepler, ayant analysé les données planétaires de Tycho Brahé, doit abandonner le mythe de la perfection circulaire, et décrit les trajectoires planétaires en termes d'ellipses [5]. En 1610 enfin, Galilée braque une lunette grossissante vers le ciel [6]; dévoilant pour la première fois l'imperfection de la Lune, constellée de cratères, et du Soleil, couvert de taches, il ouvre la voie à une physique terrestre et une physique céleste unifiées. Cette révolution cosmologique étalée sur près d'un siècle a donc vu l'éclatement du cosmos clos aristotélo-chrétien, centré sur la terre, au profit d'un espace agrandi (chez certains jusqu'à l'infini) dans lesquels la terre n'occupe qu'une place marginale.
Les révolutions scientifiques semblent devoir accompagner les révolutions sociales, politiques ou économiques. Il faut souvent de grands bouleversements de société pour oser repenser la représentation du monde. Réciproquement, un changement de paradigme scientifique engendre, de façon plus subtile et plus lente, des évolutions dans le domaine de la philosophie et de l'esthétique [7]. Ainsi, établir la position centrale du Soleil contribue à minimiser l'importance des affaires terrestres ou humaines, ce qui ne peut laisser indifférente la pensée philosophique et littéraire.
Si les révolutions cosmologiques ont tant d'influence culturelle, c'est aussi parce qu'elles vont de pair avec une refonte de la physique fondamentale. La révolution copernico-galiléenne a débouché sur l'idée d'unification des physiques terrestre et céleste, sur les lois du mouvement planétaire, et marque la naissance même de la mécanique. La révolution cosmologique newtonienne, avec son espace infini absolu et son temps éternel au sein desquels se meuvent les astres soumis à l'attraction universelle, accompagne l'énoncé des principes fondamentaux de la dynamique et la définition des forces.
La révolution cosmologique relativiste, à savoir la découverte de l'expansion de l'univers et la reconnaissance d'une évolution du cosmos dans son ensemble à partir d'une origine singulière (appelée aujourd'hui <<Big Bang>>), prend sa source dans la théorie de la relativité, élaborée par Einstein en 1905, puis en 1915. Celle-ci remanie essentiellement les concepts d'espace, de temps, de lumière et de gravitation. Dans sa version actuelle, la cosmologie relativiste repose également sur l'autre grand pilier de la physique moderne: la mécanique quantique, qui, en décrivant les interactions entre particules élémentaires et les ondes électromagnétiques, remanie les concepts de la mécanique classique.
Ainsi, le lien indéfectible entre cosmologie et concepts physiques fondamentaux ne facilite guère l'assimilation rapide des nouveaux paradigmes cosmologiques. Pour ce qui est de la révolution cosmologique relativiste, il a fallu au moins trente années pour qu'un consensus - non pas l'unanimité - commence à voir le jour chez les physiciens.
L'image qu'offre aujourd'hui la cosmologie de l'évolution de l'univers - qui est loin d'être définitive - est assez différente du schéma initialement proposé par Friedmann et Lemaître, mais les concepts fondamentaux sont restés. L'origine des grandes structures cosmiques a effectivement été trouvée dans les inhomogénéités de densité de l'univers primitif. Les traces de ces irrégularités ont été décelées en 1992 par le satellite américain COBE (COsmic Background Explorer). Dès lors, il n'y a plus guère de doutes quant à la validité de la théorie et des observations sur lesquelles les modèles cosmologiques relativistes sont fondés, même si, ça et là, de saines critiques - encore que trop vite relayées et amplifiées par les médias - paraissent encore dans la littérature spécialisée.
A l'instar des deux révolutions cosmologiques antérieures, la révolution relativiste déborde largement son strict cadre d'application astronomique. Force est de reconnaître qu'il s'agit de la théorie scientifique la plus ambitieuse de l'histoire. Comme le souligne Jacques Merleau-Ponty [8], le commandement du catéchisme réductionniste, <<Tu ne parleras pas du Tout>>, est transgressé de façon irréversible. La cosmologie relativiste parle désormais de l'univers comme d'un système physique, soumis à des lois et confronté à des faits expérimentaux. Le système <<univers>> jouit toutefois d'un statut unique. Par là-même, la cosmologie présente la particularité d'être, bien que discipline très spécialisée de la physique, en permanence commentée et critiquée par des chercheurs extérieurs à cette discipline [9].
L'objet de cette introduction n'est pas de retracer, même brièvement, l'histoire de la cosmologie à travers les siècles, ni les quelques décennies qui ont vu le développement de la cosmologie relativiste. Les études sur la question, anthologiques ou analytiques, sont nombreuses et certaines sont de qualité [10]. Nous nous proposons de présenter et d'analyser les textes qui sont à l'origine des deux idées maîtresses de la cosmologie relativiste :
- l'expansion de l'univers
- son origine singulière.
Ces textes sont l'oeuvre de deux pionniers qui, armés de leur seul <<crayon>> et d'une intuition que l'on peut sans emphase qualifier de géniale, ont dévoilé cette nouvelle vision du monde : le russe Alexandre Friedmann [11] (1888 -1925) et le belge Georges Lemaître (1894-1966). Deux de leurs textes au moins, publiés pour le premier en 1922, pour le second en 1927, en font les véritables <<pères>> du Big Bang.
Cependant, l'une des anomalies de l'histoire des sciences récente veut que dans l'esprit (et sous la plume) de nombreux écrivains scientifiques à large audience, les concepts d'univers en expansion et de Big Bang soient attribués à deux autres hommes de science: Edwin Hubble et Albert Einstein. Or, si Edwin Hubble a bien mis en évidence expérimentale la relation linéaire entre le décalage spectral vers le rouge des galaxies et la distance, il n'a ni découvert ce décalage spectral systématique (la découverte revient à Vesto Slipher), ni accepté l'interprétation relativiste de ses observations, à savoir l'expansion de l'espace en lieu et place d'un déplacement réel des galaxies. Quant au génial inventeur de la théorie de la relativité, il a rejeté pendant plus de dix ans l'idée d'univers évolutif - semble-t-il sur la foi de préjugés philosophiques-, et il a cessé de travailler dans le domaine dès lors qu'il a dû amender son opinion.
L'anonymat quasi complet de Friedmann et Lemaître auprès du grand public est une chose. La sous-estimation de leur contribution scientifique dans la communauté des physiciens, voire même dans celle des astrophysiciens et des cosmologistes, en est une autre, très surprenante si l'on songe que les concepts qu'ils ont promulgués resteront l'un des accomplissements les plus remarquables de la science du XXe siècle. Le Biographical Encyclopedia of Scientists [12] accorde une petite notice à Friedmann mais aucune à Lemaître (pour des motifs divers, notamment politiques et idéologiques, les auteurs soviétiques font l'objet de plus d'attention de la part des américains que les auteurs francophones); le dictionnaire français Inventeurs et Scientifiques [13] cite au contraire Lemaître mais non pas Friedmann ; la plus sérieuse et plus complète compilation de ce type, le Dictionary of Scientific Biography [14], accorde cependant un article à chacun, mais au développement plus que modeste eu égard à la portée de leur oeuvre.
Les raisons de ce relatif oubli sont multiples et d'importances diverses. Certes, Friedmann a publié ses oeuvres en allemand ou en russe, et la plupart des articles de Lemaître sont rédigés en français ; mais Einstein et Poincaré, pour ne citer qu'eux, ont également exprimé leurs résultats fondamentaux dans leur langue maternelle. Certes, l'érosion du temps et des mémoires fait que les dits et écrits sont rapidement déformés, parfois jusqu'à la caricature. Par exemple, l'article de revue sur la cosmologie relativiste publié par Robertson [15] dès 1933 - au demeurant excellent - est déjà trompeur sur l'histoire contemporaine qu'il décrit ; en laissant croire que le concept d'univers en expansion était déjà accepté, il traduit davantage le voeu secret de son auteur qu'une objectivité historique. Certes, Friedmann et Lemaître ne sont pas anglo-saxons, ce qui constitue aujourd'hui un handicap sérieux pour accéder à la reconnaissance scientifique internationale, qu'elle soit anthume ou posthume.
Outre ces raisons générales et un peu difficiles à apprécier, il y a des raisons particulières. Friedmann est mort prématurément, avant même que des observations astronomiques puissent étayer sa thèse. Sans cette disparition prématurée, on peut se demander jusqu'où le savant russe aurait poussé ses investigations en cosmologie relativiste. Quant à Lemaître, pourtant à l'initiative des deux avancées conceptuelles mentionnées plus haut, sa spécialité de mathématicien et son engagement religieux ont sans doute cristallisé les résistances naturelles qui accompagnent l'instauration d'une nouvelle vision du monde [16].
La situation change progressivement. Friedmann et Lemaître sont de plus en plus reconnus comme des novateurs s'inscrivant dans la lignée des Ptolémée, Copernic, Kepler, Galilée, Newton et Einstein. Depuis peu, une biographie a été consacrée à chacun [17]. Parmi les porte-parole actuels de la cosmologie anglo-saxonne, certains commencent à reconnaître le rôle fondateur joué par Friedmann et/ou Lemaître [18], y compris à travers des ouvrages de cosmologie ayant connu quelque succès populaire [19]. Les contributions respectives des hommes de science ayant participé à l'élaboration du nouveau paradigme cosmologique se clarifient enfin : Einstein a créé la théorie de la relativité générale et écrit les équations gouvernant les propriétés physico-géométriques de l'univers ; Friedmann a découvert les solutions non statiques de ces équations, décrivant la variation temporelle de l'espace, et entrevu son possible commencement dans une singularité ; Lemaître a relié l'expansion théorique de l'espace au mouvement observé des galaxies, et jeté les bases physiques du Big Bang ; Hubble, enfin, a démontré la nature extragalactique des nébuleuses spirales, et confirmé expérimentalement la loi de proportionalité entre leur vitesse de récession et leur distance.
Dans les quelques soixante-dix années d'histoire de la cosmologie relativiste, il est possible de distinguer cinq périodes [20].
- La période initiale (1917-1927) voit le développement de modèles cosmologiques relativistes quantitatifs, mais dont la signification physique, en particulier la relation avec les observations astronomiques, n'est pas comprise.
- La période de développement (1927-1945) est celle durant laquelle les aspects géométriques et dynamiques des modèles d'univers sont explorés intensivement, et l'interprétation des décalages spectraux en termes d'univers en expansion s'affirme.
- La période de consolidation (1945-1965) correspond aux développements mathématiques et à l'amélioration des données observationnelles; elle s'achève par la découverte et l'interprétation du fond diffus cosmologique. Commence alors
- la période d'acceptation (au sens de consensus, et non d'unanimité) des modèles de <<Big Bang>> [21], qui laisse la place, à partir des années 1980, à
- la période d'élargissement, dans laquelle nous nous trouvons encore, et où des modifications, pour la plupart issues de la physique des hautes énergies, sont apportées aux modèles standard de Big Bang.
Les textes présentés dans ce volume relèvent tous des deux premières périodes. Ceux de Friedmann appartiennent à la période initiale, ceux de Lemaître à la période de développement. Ce sont en fait les travaux de Lemaître qui définissent le découpage entre les trois premières périodes. Son article de 1927 inaugure en effet la période de développement, tandis que son recueil d'articles, publié en 1945 sous le nom de L'hypothèse de l'atome primitif, la clôt.
Nous avons voulu présenter en outre deux aspects différents de leur activité créatrice : des écrits de vulgarisation scientifique (de haute volée) et certains de leurs écrits techniques. Le livre de vulgarisation de Friedmann (le premier de ce genre à avoir été publié en langue russe) est traduit pour la première fois dans une langue étrangère. Ses deux articles fondamentaux de 1922 et 1924, à l'origine publiés en allemand, étaient inédits en langue française. Les correspondances Lemaître - de Sitter et Lemaître - Einstein, puisées dans les Archives Lemaître à l'Université de Louvain-la-Neuve [22], sont également inédites.
Nous l'avons dit plus haut, les textes fondateurs de la cosmologie moderne n'auraient pas vu le jour sans l'élaboration préalable de la relativité générale, qui est une théorie de la gravitation. Celle-ci constituant le sujet principal de l'ouvrage de vulgarisation de Friedmann, il nous paraît utile d'en rappeler brièvement l'historique [23].
Aristote [24] affirma qu'une force ne pouvait s'appliquer que par contact - la force à distance étant selon lui impossible. Il prétendit en outre qu'une force constante était nécessaire pour maintenir un corps en mouvement rectiligne. Cette notion manifestement fausse (sinon, les flèches retomberaient selon une ligne brisée et non pas une parabole) bloqua la compréhension des phénomènes de gravité pendant deux millénaires.
Le nouveau système du monde héliocentrique, proposé par Copernic en 1543, fit office de déclic : les planètes tournent autour du Soleil central et non l'inverse, soit ; mais qu'est-ce qui les meut ? Copernic n'y répondit point, mais dans les décennies qui suivirent, les lois du mouvement planétaire découvertes par Kepler, et celles régissant la chute des corps décrites par Galilée, fixèrent un cadre propice à l'élaboration d'une théorie de la gravitation. Celle-ci vit le jour en 1687 sous la plume d'Isaac Newton et sous le nom d'attraction universelle [25].
Après avoir reçu leur forme analytique définitive, les lois de la gravitation newtonienne furent développées sous forme de méthodes très générales et très puissantes, utilisant de nouvelles quantités reliées à la force mais éloignées de l'expérience commune, telles que le potentiel. La théorie de l'attraction universelle ne fut réellement acceptée qu'après avoir connu des confirmations expérimentales, portant notamment sur la forme du globe terrestre (1736), le retour des comètes périodiques (1759) et la découverte de nouvelles planètes (1846).
Malgré ses triomphes pratiques, l'action gravitationnelle à distance restait inexpliquée. En 1864, James Clerk Maxwell fit à ce sujet quelques remarques profondes [26]. Désireux d'expliquer l'action électromagnétique s'exerçant entre corps distants sans supposer l'existence de forces capables d'agir à distance, Maxwell fit l'hypothèse d'un champ réparti dans tout l'espace ; il remarqua alors qu'ayant rattaché les attractions et répulsions magnétiques et électriques à l'action d'un milieu environnant, et trouvé qu'elles dépendaient de l'inverse du carré de la distance, il était naturel de se demander si l'attraction gravitationnelle, qui suivait la même loi de distance, ne pouvait pas, elle aussi, être rattachée à l'action d'un milieu. Maxwell avoua toutefois son incapacité à poursuivre ses investigations sur les causes de la gravitation.
A l'aube du XXe siècle, Hendrik Lorentz mit en évidence la variation des intervalles de temps et d'espace avec la vitesse du référentiel et donna les formules de transformation entre deux référentiels à vitesse relative uniforme, qui allaient permettre le développement de la relativité restreinte ; il conjectura aussi que la gravitation pouvait être attribuée à une interaction non pas instantanée, mais se propageant à la vitesse de la lumière [27]. Dans un article de juillet 1905 (soumis quelques jours avant celui d'Einstein sur le même sujet), Henri Poincaré posa le principe de la relativité restreinte : tous les référentiels à vitesse relative uniforme sont équivalents, la forme des lois physiques étant invariante sous les transformations de Lorentz. Notant toutefois que la loi de gravitation newtonienne ne satisfaisait pas à ce critère, il proposa l'existence d'ondes gravitationnelles voyageant à la vitesse de la lumière, mais ne développa pas de nouvelle théorie.
En 1907, Einstein reprit le problème de la gravitation posé par Poincaré. Comment la gravitation newtonienne devait-elle être modifiée de façon à être compatible avec la relativité restreinte ? Il souçonna que le Principe d'Équivalence, c'est-à-dire l'égalité de la masse inertielle et de la masse gravitationnelle constatée expérimentalement, devait jouer un rôle-clé dans la gravitation. Il eut alors ce qu'il appellera plus tard <<l'idée la plus heureuse de son existence>>, à savoir qu'un observateur tombant en chute libre ne ressentirait aucun champ gravitationnel ; en d'autres termes, l'équivalence physique complète entre un champ gravitationnel et un système de référence convenablement accéléré. Cette hypothèse permettait de généraliser le principe de relativité au cas du mouvement uniformément accéléré, et faisait ressortir que le postulat de base de la relativité restreinte était trop étroit : pour décrire la gravitation, il fallait également envisager l'équivalence entre tous les référentiels en accélération relative uniforme, se traduisant par l'indépendance de la forme des lois physiques par rapport à certaines transformations non linéaires des coordonnées dans un espace à quatre dimensions.
En vertu du Principe d'Equivalence, toutes les formes d'énergie doivent être influencées par la gravitation, y compris la lumière. En 1911, l'astronome allemand Erwin Finlay Freundlich convainquit Einstein de l'importance des observations astronomiques pour tester les théories gravitationnelles, notamment la déflexion de la lumière dans un champ gravitationnel. Einstein n'avait précédemment songé qu'à des expériences terrestres, laissant peu de chances à des résultats mesurables en raison de la faiblesse du champ gravitationnel mis en jeu. Dans son article [28], il discuta également du décalage vers le rouge gravitationnel, selon lequel la lumière s'échappant d'un astre massif doit être décalée vers les plus grandes longueurs d'onde, en raison de la perte d'énergie due au champ gravitationnel.
En 1912, Einstein montra que les transformations de Lorentz étaient incompatibles avec une description non-newtonienne de la gravitation incorporant le Principe d'Equivalence. Ces recherches incitèrent d'autres physiciens à bâtir des théories gravitationnelles. Gunnar Nordström, Max Abraham et Gustav Mie effectuèrent diverses tentatives, toutes inspirées par celle d'Einstein, mais ne parvinrent pas à élaborer une théorie satisfaisante.
De son côté, Einstein comprit le fond technique du problème : si tous les systèmes de référence accélérés sont équivalents, alors la géométrie euclidienne ne peut être valide en chaque point de l'espace. Il mesura alors combien les fondements de la géométrie revêtaient une importance physique fondamentale et, dès lors, changea d'état d'esprit au sujet des mathématiques, qu'il avait jusqu'alors quelque peu négligées. Son ami Marcel Grossmann entreprit de lui expliquer les développements mathématiques récents sur les espaces courbes, obtenus par Riemann, Ricci et Levi-Civita. En 1913, Einstein et Grossmann signèrent ensemble un article en deux parties, dans lequel l'utilisation du calcul tensoriel faisait progresser le formalisme gravitationnel de manière significative. Grossmann fournit à Einstein le tenseur de courbure de Riemann-Christoffel, qui allait devenir l'outil géométrique de base de la future théorie. Pour la première fois, la gravitation était décrite en termes d'un tenseur métrique, dont les coefficients jouent le rôle de potentiels gravitationnels. Toutefois, la théorie restait incorrecte.
A la fin juin 1915, Einstein passa une semaine à Göttingen, où il donna six cours consacrés à l'exposé de sa version de la relativité générale. David Hilbert et Félix Klein assistèrent à ces cours et Einstein, après avoir quitté Göttingen, exprima sa satisfaction de les avoir convaincus.
Les dernières étapes de la théorie de la relativité générale furent accomplies simultanément par Einstein et Hilbert, qui tous deux reconnurent les erreurs figurant dans l'article d'octobre 1914.
Le 18 novembre 1915, Einstein se rendit compte que sa théorie expliquait naturellement l'avance du périhélie de la planète Mercure. En 1859, l'astronome français Urbain-Joseph Le Verrier avait en effet noté que le périhélie (le point de l'orbite où la planète est la plus proche du Soleil) avançait au cours du temps, une partie de l'avance s'expliquant par les perturbations gravitationnelles des autres planètes, une partie résiduelle de 38" par siècle restant inexpliquée en termes de ce qui était connu à l'époque. Nombre de solutions possibles avaient été proposées dans le cadre de la gravitation newtonienne, par exemple que le soleil fût très aplati, que Vénus fût 10% plus massive que ce que l'on pensait, ou bien qu'une autre planète gravitât à l'intérieur de l'orbite de Mercure - hypothèses infirmées par les observations. Restait la possibilité que la loi de Newton elle-même fût incorrecte. Depuis 1882, l'avance du périhélie était connue avec plus de précision : 43" par siècle, valeur confirmée par Freundlich en 1913. En novembre 1915, Einstein appliqua donc sa théorie de la gravitation à la description de l'orbite mercurienne, et découvrit que l'avance de 43" par siècle s'expliquait avec précision dans le cadre de sa nouvelle théorie gravitationnelle, sans invoquer l'existence de corps invisibles ou d'autres hypothèses ad hoc. L'article d'Einstein [29], daté du 18 novembre, ne présentait pas encore la forme correcte des équations du champ, mais ceci n'affectait pas le calcul particulier concernant l'orbite de Mercure.
Einstein montra aussi que le calcul de la déflexion de la lumière qu'il avait présenté dans son travail de 1911 était faux d'un facteur 2, la valeur correcte étant 1"74 (de fait, après plusieurs tentatives en vue de mesurer cette déviation qui avaient échoué pour des raisons diverses telles que le mauvais temps, la guerre, l'incompétence, etc., deux expéditions britanniques confirmeront en 1919 la prédiction d'Einstein, en fournissant les valeurs 1"98± 0"30 et 1"61± 0"30).
Le 25 novembre 1915, Einstein soumit son article fondamental Les équations du champ de la gravitation [30], fixant la forme correcte de la relativité générale. Les calculs de la déflexion des rayons lumineux et de l'avance du périhélie de Mercure restaient identiques à ceux effectués une semaine auparavant.
Le 20 novembre, Hilbert avait lui aussi soumis son article, Grundlagen der Physik, fournissant les équations correctes de la gravitation. Il apportait des contributions importantes à la relativité ne se trouvant pas dans le travail d'Einstein. Hilbert appliquait les principes variationnels à la gravitation, et donnait sans démontration un ensemble d'identités remarquables qu'il attribuait à la mathématicienne Emmy Noether [31]. L'article de Hilbert énonçait aussi l'espoir d'une unification géométrique de la gravitation et de l'électromagnétisme.
Immédiatement après, Karl Schwarzschild découvrit une solution mathématique exacte des équations, correspondant au champ gravitationnel créé par un corps sphérique massif. Ce travail, à l'origine purement théorique et qui allait longtemps rester incompris, deviendrait plus tard la pierre de touche de la compréhension des étoiles à neutrons, des pulsars et des trous noirs.
En 1916, Einstein publia un article expliquant les fondements de la relativité générale en termes plus aisément compréhensibles [32]. Le terrain théorique était désormais prêt pour la cosmologie.
Il était légitime que le père de la relativité générale cherchât en premier lieu une solution cosmologique des équations du champ. L'ère de la cosmologie relativiste commence donc par la publication en 1917 de l'article d'Einstein, <<Kosmologische Betrachtungen zur allgemeinen Relativitätstheorie>> [33]. Ce texte fondamental a été traduit en français et analysé dans un autre volume de cette collection [34], mais compte tenu de son importance, nous le commentons ci-après.
La croyance en un univers statique, c'est-à-dire invariable dans le temps, subsistait encore. Aussi Einstein envisage-t-il tout naturellement un univers rempli de matière sans pression, de densité constante dans l'espace et dans le temps. Distribution de matière uniforme implique courbure uniforme; la partie spatiale de l'univers d'Einstein a donc une courbure positive, partout la même - c'est un espace de type sphérique. L'univers d'Einstein peut s'interpréter mathématiquement comme le produit d'une hypersphère par un axe temporel infini. Son mérite est au moins double ; en premier lieu, il démontre l'efficacité technique de la relativité générale pour aborder le problème cosmologique ; en second lieu, il ébranle la croyance en un univers infini en proposant un espace fini mais sans limite.
Mais si Einstein a osé toucher à l'espace, il n'a pas osé toucher au temps. Là réside le défaut fatal de son modèle cosmologique : l'univers d'Einstein, c'est de la matière sans mouvement. Nombre de commentateurs ont par la suite écrit qu'Einstein n'avait pu se défaire d'une influence <<culturelle>> et <<philosophique>> remontant à Aristote, selon laquelle le cosmos serait immuable. C'est éluder certaines motivations plus pragmatiques du physicien théoricien.
Einstein sait que les étoiles ont de faibles mouvements propres, et il
présume qu'il n'existe pas d'autre mouvement séculaire à
grande échelle. Les observations de l'époque ne fournissent
aucune contre-indication claire à cette hypothèse, et la nature
extragalactique des nébuleuses spirales n'est même pas
élucidée. Il est donc légitime de considérer
l'univers comme un simple gaz d'étoiles, et Einstein tient le
raisonnement suivant. Si l'univers est infini à la fois dans l'espace et
dans le temps, ainsi que le propose la cosmologie newtonienne, alors pour
compléter les équations de la relativité
générale il est nécessaire de spécifier des
conditions aux limites à l'infini. Influencé par une idée
de Mach [35] selon laquelle une particule
unique dans un espace vide de matière n'aurait pas d'inertie, Einstein
estime que l'inertie est engendrée par la distribution des masses
lointaines. Or, les potentiels gravitationnels (les coefficients
![]() de la métrique) sont déterminés par la distribution de la
matière. Pour que l'inertie reste finie, il faut donc que les
coefficients de la métrique s'annulent à l'infini; mais puisque
l'espace n'existe pas sans la gravitation, cela implique la disparition pure et
simple de l'espace à l'infini. Einstein abandonne donc le modèle
d'un univers spatialement infini, et tente de trouver une solution de ses
équations décrivant un univers fini, empli d'une distribution
statique de matière. Il est à ce moment-là troublé
par le résultat newtonien bien connu selon lequel un tel
équilibre est instable à la moindre perturbation. L'un de ses
arguments est particulièrement intéressant car il utilise une
forme de raisonnement relevant de la mécanique statistique, en laquelle
il est passé maître. Einstein envisage l'univers fini comme un gaz
de Boltzmann en équilibre à une certaine température
finie, dont les molécules sont les étoiles. Si le nombre
d'étoiles par unité de volume doit s'annuler à la
frontière de la distribution, argumente Einstein, elle doit aussi
s'annuler au centre. En effet, le rapport des densités au bord et au
centre est égal au rapport des facteurs de Boltzmann,
exp(-E/kT), mettant en
jeu la différence des potentiels gravitationnels aux deux points de
référence. Or cette différence ne peut pas s'annuler, sauf
si la densité est partout nulle. Ceci contredit l'hypothèse que
la densité stellaire moyenne de l'univers est une constante strictement
positive. Einstein en déduit avec justesse que la relativité
générale, dans sa formulation originale, est incompatible avec un
univers statique.
de la métrique) sont déterminés par la distribution de la
matière. Pour que l'inertie reste finie, il faut donc que les
coefficients de la métrique s'annulent à l'infini; mais puisque
l'espace n'existe pas sans la gravitation, cela implique la disparition pure et
simple de l'espace à l'infini. Einstein abandonne donc le modèle
d'un univers spatialement infini, et tente de trouver une solution de ses
équations décrivant un univers fini, empli d'une distribution
statique de matière. Il est à ce moment-là troublé
par le résultat newtonien bien connu selon lequel un tel
équilibre est instable à la moindre perturbation. L'un de ses
arguments est particulièrement intéressant car il utilise une
forme de raisonnement relevant de la mécanique statistique, en laquelle
il est passé maître. Einstein envisage l'univers fini comme un gaz
de Boltzmann en équilibre à une certaine température
finie, dont les molécules sont les étoiles. Si le nombre
d'étoiles par unité de volume doit s'annuler à la
frontière de la distribution, argumente Einstein, elle doit aussi
s'annuler au centre. En effet, le rapport des densités au bord et au
centre est égal au rapport des facteurs de Boltzmann,
exp(-E/kT), mettant en
jeu la différence des potentiels gravitationnels aux deux points de
référence. Or cette différence ne peut pas s'annuler, sauf
si la densité est partout nulle. Ceci contredit l'hypothèse que
la densité stellaire moyenne de l'univers est une constante strictement
positive. Einstein en déduit avec justesse que la relativité
générale, dans sa formulation originale, est incompatible avec un
univers statique.
L'idée qu'il puisse exister des solutions non statiques l'effleure, puisque selon ses propres mots, <<le caractère courbe de l'espace varie dans le temps et dans l'espace en fonction de la distribution de la matière>> [36]. Il n'abandonne pas pour autant l'hypothèse de staticité, puisqu'il pense que les observations (et non pas la physique d'Aristote) l'exigent. Il n'a par conséquent pas d'autre choix que de modifier la formulation originale, en introduisant la constante cosmologique, notée l
Le seul terme qu'il soit possible d'ajouter aux équations du champ tout
en respectant le postulat de covariance est proportionnel au tenseur de
métrique, le facteur de proportionnalité étant la
constante l. Si, formellement, ce nouveau terme peut être
incorporé dans le tenseur impulsion-énergie [37],
pour Einstein il doit être considéré comme d'origine
physique différente; non pas lié à la matière, mais
à la structure même de l'espace, d'où son qualificatif
<<cosmologique>>. Ayant modifié ses équations,
Einstein s'attache ensuite à trouver une solution satisfaisant ses
hypothèses relatives au champ et à la matière. Il commence
par construire un tenseur métrique. Les conditions qu'il pose sont que
la composante temporelle est indépendante de l'espace, que le tenseur
métrique est diagonal, et que l'espace est à courbure constante -
cette dernière condition correspondant à l'hypothèse d'une
distribution uniforme de la matière. Pour garantir la finitude de
l'espace, Einstein choisit la géométrie spatiale la plus simple,
celle de l'hypersphère de <<rayon>> R, dont la courbure
constante est positive. La solution obtenue est connue sous le nom d'univers
cylindrique d'Einstein. Si l'on représente la direction du temps par un
axe vertical et que l'on trace un cylindre dont l'axe est confondu avec le
temps, on obtient une description projective de l'espace d'Einstein dans
laquelle deux directions d'espace ont été supprimées. Le
cercle représente le périmètre de l'espace
sphérique à un instant donné, et ce
périmètre ne varie pas au cours du temps. C'est donc un espace
authentiquement statique. Muni de cette métrique, Einstein peut
étudier les conditions d'existence de solutions de ses équations.
Il y a deux conditions, l'une reliant la constante cosmologique à la
densité de matière, l'autre la reliant au rayon de courbure de
l'espace:
![]() .
.
Malgré la remarque d'Einstein à propos du terme cosmologique : <<ce dernier n'est nécessaire que pour rendre possible une répartition quasi statique de la matière, laquelle correspond au fait que les vitesses des étoiles sont petites>> [38], la présence possible d'une constante cosmologique dans les équations du champ peut être envisagée indépendamment du modèle statique spécifique d'Einstein. La même année 1917, l'astronome hollandais Wilhem de Sitter découvre une deuxième solution cosmologique des équations de la relativité générale [39]. Il s'agit encore d'une solution statique, en ce sens qu'il existe un système de coordonnées dans lequel tous les coefficients de la métrique sont indépendants du temps, avec constante cosmologique (si celle-ci est égale à zéro, l'espace de de Sitter se réduit à l'espace plat de Minkowski, solution unique de la relativité restreinte). Elle se distingue de celle d'Einstein par le fait qu'elle ne contient pas de matière. Plus précisément, les formes de matière qui emplissent l'univers de de Sitter, telles que les étoiles, sont considérées comme des <<particules-test>> n'engendrant pas de gravitation. A ce titre, elles sont en mouvement dans une métrique de fond fixée d'avance.
La solution de de Sitter est caractérisée par
![]()
Mais pour l'heure, il ne s'agit encore que de <<curiosités mathématiques>>; la métrique de de Sitter ne peut sérieusement être considérée comme un modèle d'univers plausible, puisque les propriétés de l'espace-temps y sont indépendantes de la matière. C'est du moins l'opinion d'Einstein, pour qui le Principe de Mach, nous l'avons vu, impose que les coefficients de la métrique soient déterminés par la distribution de matière [41]. La vraie résolution du dilemme est trouvée en 1922 par le mathématicien, mécanicien et météorologue russe Friedmann.
Alexandre Alexandrovich Friedmann [42] est né à Saint-Petersbourg (Russie) en 1888. Son père, Alexandrovich Friedmann, était danseur dans le ballet du théâtre Mariinsky; sa mère, L.I. Voyachek, était pianiste. En 1910, Friedmann obtient son diplôme de l'université de Saint-Petersbourg dans la spécialité <<physique mathématique>>. Entre 1914 et 1916 il participe à la première guerre mondiale, effectuant des missions à bord d'avions militaires de l'armée russe, au titre d'expert en balistique et en techniques de bombardement. Entre 1918 et 1920 il est professeur à l'université de Perm, et, entre 1920 et 1924, professeur à l'université de Petrograd (nouveau nom donné à Saint-Petersbourg). Il y enseigne la physique et les mathématiques. C'est au cours de cette période qu'il découvre la théorie de la relativité générale et entreprend d'en chercher des solutions exactes. Il rédige son ouvrage de vulgarisation, L'Univers comme Espace et Temps, qui paraît en 1923. Ses deux grands articles cosmologiques datent de 1922 et de 1924. En 1925, il est nommé directeur de l'institut géophysique de Leningrad (le nom de Saint-Petersbourg avait à nouveau changé en 1924). L'été 1925, en compagnie de l'aviateur P.F. Fedosenko, il bat le record d'altitude en ballon stratosphérique en s'élevant à 7400 m. Friedmann meurt subitement à Leningrad le 16 septembre 1925, d'une fièvre typhoïde [43].
Il est enterré dans sa ville natale. A ce propos, une anecdote instructive mérite d'être contée. L'emplacement de la tombe du savant russe a rapidement été oublié, d'autant que le régime stalinien qui a suivi n'a guère été enclin à perpétuer la mémoire de ce savant réputé <<créationniste>>. En 1988, le Laboratoire Alexandre Friedmann de l'université Saint Petersbourg décide d'organiser le premier <<Séminaire International A.Friedmann de Cosmologie>>, pour honorer le centenaire de la naissance du savant. Le directeur de l'institut Friedmann, Andrey Grib, a l'idée de faire rechercher la tombe d'Alexandre Friedmann, prévoyant une petite cérémonie commérative à laquelle les participants des divers pays seraient curieux de participer. Un vénérable professeur de l'institut de physique et de technologie de Saint-Petersbourg, et ancien élève de Friedmann, Georgy Grinberg, se souvient avoir assisté aux funérailles du savant au cimetière Smolenskoye, et que la tombe du cosmologiste était proche de celle du grand mathématicien Leonhard Euler. Andrey Grib demande donc à l'un de ses étudiants, Mihail Rosenberg, de se rendre au cimetière pour repérer la tombe - lui laissant même entendre que cette tâche ferait partie de son travail de thèse. Lorsque Mihail Rosenberg arrive au cimetière Smolenskoye et demande à consulter le registre de toutes les personnes enterrées ici, les autorités lui répondent qu'elles n'ont aucune information antérieure à la seconde guerre mondiale. Rosenberg demande à voir la tombe de Leonhard Euler. Après la guerre, lui répond-on, cette dernière a été transférée dans un autre cimetière. Reste au moins l'ancien emplacement, que les autorités lui indiquent. Rosenberg cherche aux alentours mais ne trouve aucun indice de la présence de Friedmann. Il commence alors à se quereller avec les autorités: comment les archives peuvent-elles avoir disparu ? A ce moment, un préposé à l'entretien des tombes s'approche et s'enquiert de l'objet de la dispute. Le directeur du cimetière lui répond que l'étudiant cherche un certain Friedmann ... <<Quel Friedmann? >> demande l'employé, <<Celui qui a découvert la solution cosmologique non statique des équations d'Einstein?>>. <<Oui, oui!>> s'écrie l'étudiant. <<Hé bien venez avec moi, je vais vous montrer!>> C'est ainsi que la tombe du cosmologiste a été retrouvée. Le croque-mort n'était autre qu'un ancien physicien qui avait dû quitter son institut faute de crédits.
Coupés de la littérature scientifique mondiale pendant les années de guerre et la révolution russe, les savants soviétiques ne prennent connaissance de la théorie de la relativité générale qu'avec plusieurs années de retard. En 1919, la confirmation expérimentale de la valeur de la déflexion des rayons lumineux dans le champ gravitationnel solaire, prédite par la théorie relativiste, a un grand retentissement. Dès sa nomination à l'université de Saint-Petersbourg, Friedman commence à étudier la relativité générale avec une diligence exceptionnelle. Indubitablement, la théorie le séduit par la largeur de ses vues, par sa base théorique claire et simple, son appareil mathématique élégant. Il mesure vite qu'avec cette nouvelle interprétation de la gravitation, dans laquelle la nature de l'espace et du temps est liée à la distribution et au mouvement des masses gravitantes, la structure de l'univers devient pour la première fois l'objet d'une analyse scientifique exacte.
Un séminaire régulier est organisé à l'institut de physique de l'université. Friedmann et son collègue Vsevolod Konstantinovich Frederiks donnent des leçons sur la relativité générale. Selon le physicien Vladimir Fock, qui a participé au séminaire, les styles de leurs présentations sont différents. Frederiks met l'accent sur l'aspect physique de la théorie et, n'aimant pas les formulations mathématiques, il tente de rendre ses présentations qualitatives. Friedmann place au contraire l'accent sur les mathématiques et non pas sur la physique, s'efforçant à la rigueur et à l'exhaustivité dans la formulation et la discussion des problèmes. Yuri Alexandrovitch Krutkoff, qui jouera un rôle important dans la diffusion des travaux de Friedmann, prend également part au séminaire et y donne des exposés.
En 1922, le premier travail de synthèse en langue russe sur les fondements de la relativité générale est publié par Frederiks [44]. Il est fondé sur les notes de cours délivrés par Frederiks à Petrograd et à Moscou.
A la même époque, Friedmann et Frederiks commencent à rédiger une monographie fondamentale sur la théorie de la relativité. Ils entreprennent de présenter la théorie dans toute sa rigueur logique, en supposant que le niveau de connaissance de leurs lecteurs en mathématiques et en physique théorique ne dépasse pas celui délivré dans les universités russes. Des contraintes techniques les conduisent à diviser leur projet en cinq volumes séparés : un premier volume consacré aux fondements du calcul tensoriel, un second consacré aux fondements de la géométrie multidimensionnelle, un troisième à l'électrodynamique, un quatrième et un cinquième aux fondements de la relativité restreinte et générale. Seul le premier volume [45] voit le jour; il est publié en 1924 à Leningrad par les éditions Academia.
Parallèlement, Friedmann mène à bien son propre ouvrage Mir kak prostranstvo i vremya (L'Univers comme Espace et Temps). Cet ouvrage de 131 pages sort en édition séparée à Petrograd en 1923, dans la série <<Culture Contemporaine>> proposée par Academia. Le tirage, de 3000 copies, est normal pour l'époque. Une seconde édition sera publiée 42 ans plus tard à Moscou, chez Nauka, avec un tirage de 45 000 exemplaires. Une troisième édition verra le jour en 1966, intégrée dans la collection des >Oeuvres Choisies de A. A. Friedmann.
Le livre comporte une introduction et trois chapitres respectivement intitulés l'espace, le temps, la gravitation. Il s'agit essentiellement d'un exposé axiomatique de la théorie de la relativité générale, Friedmann n'abordant la question cosmologique comme domaine d'application particulier de la théorie que dans les derniers paragraphes du dernier chapitre.
Dès l'introduction, Friedmann se défend d'avoir écrit un ouvrage de vulgarisation scientifique. Il n'appréciait visiblement guère le genre, bien qu'il possédât plusieurs ouvrages de ce type dans sa bibliothèque personnelle. Selon lui, la relativité est un sujet à la mode, mais <<impossible à vulgariser>>. Dans un pays émergeant à peine de bouleversements gigantesques, où la vie reprend son cours normal après tant d'années de guerre et de famine, l'intérêt du public pour la théorie de la relativité est un phénomène surprenant qui doit être attribué à un effet de mode. Dans son roman Sylvia, Emmanuel Berl écrit : <<La guerre avait laissé un certain désespoir au coeur de chacun ; l'après-guerre fut, néanmoins, une époque d'espérance, de foi secrète [...] Les toniques, après tout, ne manquaient pas : les révolutionnaires avaient Lénine, les industriels avaient Ford, les savants Einstein, les psychologues Freud>> [46]. Cependant, un autre facteur culturel a joué. La cosmologie traite des éternelles questions sur la nature du monde, et offre un champ de réflexion sur la place de l'homme dans l'univers. Ce n'est donc pas sans raison si, dès cette époque, les conférences publiques sur la théorie de la relativité attirent un large public, et si livres et articles sont rapidement vendus malgré l'importance de leurs tirages.
En 1923 existaient déjà une vingtaine d'ouvrages sur la relativité en langue russe. La moitié d'entre eux étaient des traductions d'ouvrages étrangers - surtout allemands. Celui d'Einstein lui-même, Relativity : the Special and the General Theory. Popular Exposition, avait connu plusieurs éditions en russe, dont deux publiées à Petrograd en 1921 et 1922. L'édition allemande de 1916 se trouvait dans la bibliothèque personnelle de Friedmann. On comptait également le livre de Freundlich, Fondements de la Théorie de la Gravitation d'Einstein, préfacé par Einstein, dont la traduction russe fut éditée par Frederiks; celui de I. Lehmann, Théorie de la Relativité; de E. Cassirer, Théorie de la Relativité d'Einstein; et de Max Born, Théorie de la Relativité. Les monographies de Charles Nordmann et Henri Bergson étaient également disponibles en traduction russe.
Malgré l'avertissement de son auteur, L'Univers comme Espace et Temps est bien un texte de vulgarisation scientifique, rédigé non pas à l'intention du grand public, mais à celle des philosophes. Telle est du moins l'ambition de Friedmann, puisque son texte était initialement destiné à la revue de philosophie Mysl (La Pensée). On ignore la raison pour laquelle il ne fut pas publié dans cette revue; il est vrai qu'un article de 131 pages n'est pas d'un format convenant à une revue. On peut également penser que le contenu et le niveau n'étaient pas adaptés. Quoi qu'il en soit, force est de reconnaître que son projet de <<vulgarisation à l'usage des philosophes>> n'est pas une réussite parfaite. Le style proprement littéraire de Friedmann est emprunté, souffrant d'un grand nombre de répétitions [47], de lourdeurs et de raideurs de langage. Quant au contenu et au niveau de technicité, Friedmann est quelque peu naïf de croire que les philosophes pourront pénétrer les arcanes de la relativité en le lisant.
L'intérêt de l'ouvrage réside ailleurs. A notre regard d'aujourd'hui, il tient en quatre points :
1) l'exposé axiomatique des problèmes de l'espace, du temps et de la gravitation,
2) la discussion de la tentative d'unification géométrique de la gravitation et de l'électromagnétisme, due à Weyl,
3) l'affirmation selon laquelle la <<création de l'univers>> apparaît naturellement comme solution des équations du champ gravitationnel,
4) les remarques sur l'indétermination topologique de la relativité générale.
Examinons ces points un par un.
Friedmann conduit le lecteur au coeur même du sujet (la nature de l'espace et du temps) par le biais de l'axiomatique et non de la physique. Cette approche particulière est celle de David Hilbert (1862-1943).
La nécessité d'une axiomatisation, des mathématiques d'abord, puis de la physique, prend sa source au milieu du XIXe siècle lorsque l'édification de la géométrie non-euclidienne hyperbolique par Gauss, Lobatchevski et Bolyai a obligé à abandonner les prétentions à la vérité absolue de la géométrie euclidienne. Dès lors, les axiomes mathématiques n'apparaissent plus comme évidents, mais comme des hypothèses dont il faut vérifier qu'elles sont adaptées à la représentation du monde sensible. Gauss est, par exemple, convaincu que le débat entre les diverses géométries peut être tranché par l'expérience; comme Friedmann le rappelle dans son livre, Gauss a même tenté de le prouver en testant la géométrie de l'espace au moyen de mesures géodésiques. Friedmann cite également à plusieurs reprises la célèbre dissertation inaugurale de Riemann, Des hypothèses qui servent de fondement à la géométrie (1867). L'ambition de Riemann est précisément de fournir un cadre mathématique général aux divers phénomènes naturels : dans la mesure où il ne peut plus y avoir de confiance illimitée en l'intuition géométrique classique, défaillante, il faut axiomatiser la géométrie sans faire appel à l'intuition. Le plus célèbre achèvement de l'axiomatisation de la géométrie euclidienne sont les Grundlagen der Geometrie [48] de Hilbert, parus en 1899. Cet ouvrage devient presque aussitôt la <<charte>> de l'axiomatique moderne. Non content de procurer un système complet d'axiomes valides pour la géométrie euclidienne, Hilbert classe ces axiomes en divers groupes de nature différente, et s'attache à déterminer la portée exacte de chacun de ces groupes d'axiomes. Par exemple, les géométries non-euclidiennes de Lobatchevski et de Riemann apparaissent comme de simples cas particuliers obtenus en supprimant ou en modifiant tel ou tel axiome. Hilbert met ainsi clairement en relief la liberté dont dispose le mathématicien dans le choix de ses hypothèses. Cette vue sera rapidement adoptée de façon à peu près unanime par les mathématiciens ; elle se développera tout au long de la première moitié du siècle, sera momentanément couronnée par l'oeuvre de Bourbaki [49], puis définitivement limitée par celle de Gödel [50].
Hilbert pousse plus loin sa réflexion en prétendant axiomatiser l'ensemble de la physique. C'est en effet l'époque où la physique s'enracine définitivement dans les mathématiques, et l'analyse critique des fondements logiques de la seconde devait nécessairement se reporter sur la première. En 1915, Hilbert publie Grundlagen der Physik (où il fournit notamment les bonnes équations de la relativité générale, comme nous l'avons dit plus haut). C'est dans ce climat que Friedmann rédige son opuscule sur la relativité.
Dès les premiers paragraphes, Friedmann insiste sur le problème de l'interprétation physique. Les mathématiciens sont en effet embarrassés par les concepts nouveaux jusqu'à ce qu'ils puissent en donner une interprétation sensible. Il en avait été ainsi des nombres négatifs et des nombres imaginaires. Au XIXe siècle, les mathématiciens avaient commencé à sentir nettement qu'il était légitime de raisonner sur des objets n'ayant aucune interprétation sensible. Par exemple, dans sa dissertation inaugurale, Riemann avait pris soin de ne pas parler de points, mais de <<déterminations>>, les relations métriques ne pouvant <<s'étudier que pour des grandeurs abstraites et se représenter que par des formules.>> [51] A cause des multiples interprétations ou modèles possibles, on avait reconnu que la nature des objets mathématiques était au fond secondaire. L'essence des mathématiques apparaissait désormais comme l'étude des relations entre des objets qui ne sont plus connus et décrits que par quelques-unes de leurs propriétés, celles précisément que l'on met à la base comme axiomes de la théorie. C'est la thèse à laquelle Friedmann adhère pleinement.
Le physicien russe utilise également le terme <<arithmétisation>>, qui peut surprendre le lecteur. Qu'a à voir l'arithmétique avec la relativité? Là encore, le contexte de l'époque doit être rappelé. L'arithmétique traite des entiers naturels, <<produits exclusifs de notre esprit>> comme l'écrivait Gauss en 1832 en les opposant à la notion d'espace [52]. Weierstrass a toutefois obtenu un modèle des nombres rationnels positifs ou des nombres entiers négatifs en considérant des classes de couples d'entiers naturels. Puis Cantor et Dedekind ont réussi à trouver un modèle arithmétique des nombres irrationnels. A partir de ce moment, les entiers sont devenus le fondement de toutes les mathématiques classiques. Les réels ont été interprétés en termes d'entiers, les nombres complexes et la géométrie euclidienne aussi (grâce à la géométrie analytique); enfin, Beltrami et Klein ont obtenu des modèles euclidiens des géométries non-euclidiennes de Lobatchevski et Riemann, et par suite arithmétisé ces théories.
Les modèles fondés sur l'arithmétique ont acquis d'autant plus d'importance que la méthode axiomatique s'est développée, et avec elle la conception des objets mathématiques comme libres créations de l'esprit. Démontrer l'existence d'un objet mathématique ayant des propriétés données, c'est simplement construire un objet ayant les propriétés indiquées. C'est à quoi servent les modèles arithmétiques. On parle alors de la classe des objets possédant telle ou telle propriété. Dans son "calcul logique", Boole [53] n'avait pas hésité à introduire en 1847 l'Univers comme ensemble de tous les objets!
C'est bien ainsi que Friedmann définit l'espace et le temps : en termes de classe d'objets arithmétisée au moyen de telle ou telle propriété. Il est clair que l'axiomatisation de l'espace et du temps a peu de vertu pédagogique ; ce qui constitue l'une des originalités - sur le plan physique et non pas mathématique - de la présentation de Friedmann en constitue donc, aussi, l'une des limites.
La théorie de la relativité restreinte - à l'origine conçue comme une théorie physique de l'électrodynamique - a été géométrisée par Hermann Minkowski en 1908. C'est en effet lui qui introduisit le formalisme d'espace-temps quadri-dimensionnel, base mathématique de tous les développements relativistes futurs. Historiquement, la relativité générale a été construite comme une théorie géométrique de la gravitation [54]; cette dernière n'est plus décrite en termes de force, mais en termes de métrique d'un espace riemannien.
Hermann Weyl fut le premier à tenter d'étendre la géométrie riemannienne de façon à incorporer l'électromagnétisme et la gravitation dans un formalisme unifié. Il utilisa des connexions non métriques, mais sa tentative s'avéra plus tard un échec sous sa forme originelle. Néanmoins, la théorie était belle. Pour son aspect mathématique, elle a joué un rôle essentiel dans le développement de la géométrie différentielle moderne et dans l'élaboration des théories de jauge [55]. Quant à sa motivation physique, elle prolongeait le voeu exprimé par Hilbert dans son article de 1915, et allait hanter sans résultat l'esprit des physiciens tout au long de ce siècle : traiter toutes les forces de la Nature (et pas seulement la gravitation) comme des manifestations de la structure d'un espace-temps.
L'importance fondamentale de ces questions se reflète dans la place que Friedmann accorde à l'approche de Weyl. Tout en reconnaissant que la théorie n'est en aucune façon prouvée par l'expérience, le physicien russe laisse transparaître une certaine préférence pour l'approche de Weyl par rapport à celle, plus modeste, d'Einstein.
Il est intéressant de préciser quel allait être le sort des tentatives de géométrisation de l'électromagnétisme après 1922. On peut distinguer deux approches : soit la généralisation de la géométrie de l'espace-temps à quatre dimensions - voie empruntée par Weyl, Eddington, Cartan et Einstein -, soit l'adjonction d'une dimension supplémentaire à l'espace-temps - parti adopté par la théorie de Kaluza-Klein.
En ce qui concerne la première voie, le mathématicien français Elie Cartan proposa en 1922 une extension de la géométrie riemannienne utilisant des connexions qui n'étaient pas nécessairement symétriques sur ses deux indices inférieurs. Il suspecta que le tenseur obtenu de cette façon, aujourd'hui appelé torsion de Cartan, pouvait être en rapport avec l'électrodynamique. Dans ce contexte, les lettres sur le parallélisme absolu échangées entre Cartan et Einstein [56] dans la période 1922-1929, sont très intéressantes (le nom de parallélisme absolu vient du fait que dans cette théorie, le tenseur de courbure de Riemann, distinct du tenseur de Riemann-Christoffel utilisé en relativité générale, est partout nul). A leur suite, Einstein publia une série d'articles dans les rapports de l'Académie des Sciences de Prusse au sujet du parallélisme absolu et d'une théorie du champ unifiée. L'un d'entre eux récapitule les divers articles proposant des équations du champ qui incluent le tenseur de torsion et conduisent, en première approximation, à la fois aux équations de Maxwell et aux équations de Newton-Poisson [57]. Malheureusement, Einstein n'essaya jamais d'incorporer la mécanique quantique dans son schéma. Les autres physiciens préférèrent explorer la voie de la théorie quantique des champs plutôt que de le suivre dans son approche. Ainsi le projet de théorie unitaire d'Einstein, manquant d'une description des particules, échoua-t-il.
La deuxième voie fut empruntée par le physicien autrichien Theodor Kaluza (1885 - 1945) et le physicien suédois Oscar Klein (1894-1977). Ils développèrent indépendamment une théorie de l'espace à cinq dimensions portant aujourd'hui leur nom [58]. Dans leur modèle, la description de l'électromagnétisme nécessite l'introduction d'une <<cinquième>> dimension. Cette dimension n'est toutefois pas orthogonale à <<notre>> espace-temps quadri-dimensionnel. Les quatre cosinus directeurs des <<angles>> que fait cette nouvelle dimension avec nos dimensions usuelles dépendent du point de l'espace-temps, et forment les quatre composantes du potentiel-vecteur du champ électromagnétique. Du point de vue de cette théorie, les particules chargées se meuvent dans un espace-temps penta-dimensionnel, tandis que nous, êtres humains, ne percevons que la projection de ce mouvement dans l'espace-temps quadri-dimensionnel. Ceci peut être illustré par l'analogie avec le mouvement de l'ombre d'un avion à la surface de la Terre [59]. Le mouvement de l'ombre dépend non seulement de la trajectoire de l'avion, mais aussi de la position du Soleil dans le ciel. Donc, même si la trajectoire de l'avion est rectiligne, le mouvement de son ombre ne l'est pas. Il en va de même dans la théore de Kaluza-Klein ; la projection du mouvement varie selon les points de l'espace-temps, et l'<<ombre>> de la charge ne se meut pas selon une ligne droite. Cette déviation géodésique est interprétée comme un effet des forces électriques et magnétiques.
Le modèle de Kaluza-Klein, abandonné pour l'électromagnétisme, a été repris et généralisé dans les théories modernes de la physique des particules, en particulier dans la théorie des supercordes, où le nombre de dimensions supplémentaires atteint sept ou même davantage [60]. Ces dimensions supplémentaires sont différentes des dimensions spatiales usuelles en ce sens qu'elle sont compactifiées, c'est-à-dire qu'elles prennent la forme d'un cercle dans le plan, de rayon aussi petit que 10-33 centimètre.
Friedmann travaillera en 1924 avec le mathématicien hollandais Jan Arnoldus Schouten sur un modèle géométrique de l'électromagnétisme inspiré de celui de Weyl [61]. Ce n'est toutefois pas dans cette voie que Friedmann fut novateur, mais dans celle qui suit.
A la fin de son livre, Friedmann présente, bien que de façon fort brève, les solutions dynamiques qu'il a découvertes et publiées sous forme technique en 1922 dans Zeitschrift für Physik ; c'est donc, dans l'histoire de la cosmologie, la première formulation vulgarisée des concepts d'univers en expansion ou en contraction et de singularité cosmique. Pour ce qui est de la dynamique cosmique, Friedmann écrit : <<Le type d'univers variable engendre une famille beaucoup plus générale de modèles : dans certains cas le rayon de courbure de l'univers part d'une certaine valeur et augmente constamment au cours du temps; dans d'autres cas le rayon de courbure varie de façon périodique, l'univers se contractant en un point (de volume nul), puis, à partir de ce point, augmente de rayon jusqu'à une certaine valeur maximale, puis diminue à nouveau pour redevenir un point, et ainsi de suite>>. Ainsi, il est évident que dès la rédaction de son livre, Friedmann connaissait déjà les espace-temps fermé et ouvert, et qu'il mesurait totalement les implications de leur découverte pour l'univers réel.
Contrairement à ce qui a été souvent prétendu, le travail cosmologique de Friedmann ne se réduisait pas à un simple problème mathématique. En ce qui concerne la singularité cosmique (l'univers réduit à un point), Friedmann pose pour la première fois le problème du début et de la fin de l'univers en termes scientifiques [62]. Il ne peut s'empêcher d'y voir une implication métaphysique, lorsqu'il écrit : <<On peut se souvenir ici de la mythologie indienne sur les cycles de vie, on peut aussi parler de la création du monde à partir de rien>>. Ce terme de <<création du monde>>, une fois lancé dans le champ de la cosmologie relativiste, allait susciter bien des remous et malentendus, et bloquer psychologiquement la plupart des physiciens.
Dans la bibliographie générale d'A. Friedmann, on note l'existence d'un manuscrit perdu, justement intitulé Création (Mirozdanie). Nul ne sait quel pouvait en être le contenu, mais il n'est pas impossible que Friedmann y ait développé un point de vue théologique - point de vue qu'il se refuse à aborder dans son livre de vulgarisation, comme il le dit à plusieurs reprises. Parler de la création de l'univers sous le régime communiste était quelque peu osé politiquement, bien que Friedmann ne se souciât guère de politique. Ce n'est que dans les années 1960 que la science soviétique s'est convertie à la conception du Big Bang. Certains indices laissent à penser que si le savant russe avait survécu plus longtemps à sa théorie, il aurait pu être emprisonné et persécuté [63]
Friedmann discute également de l'âge de l'univers : <<Si on essaye de calculer le temps écoulé depuis le moment où l'univers fut créé à partir du vide jusqu'à aujourd'hui, c'est-à-dire calculer le temps depuis la création du monde, on obtient des nombres correspondant à quelques dizaines de milliards de nos années usuelles>>. Friedmann se fonde en fait sur le calcul théorique de la période d'expansion-contraction de sa solution "cyclique", qu'il a effectué dans son article de Zeitschrift für Physik (formule (14)). La période y est liée à la masse totale de l'univers et à la constante cosmologique. En tenant compte de certaines données observationnelles de l'époque relatives à la densité moyenne d'étoiles et à la taille de l'univers observable, Friedmann adopte la valeur de 5x 10^(21) masses solaires pour la masse de l'univers. En négligeant la constante cosmologique, il en déduit un âge de l'ordre de 10^(10) années. Ce nombre était beaucoup plus grand que l'âge des plus vieux objets de l'univers connu à l'époque. Au début des années 1920, l'âge de la Terre, estimé d'après la période de désintégration du radium, ne dépassait pas le milliard d'années. Comme nous aurons l'occasion de le voir plus loin, les chiffres avancés aujourd'hui pour l'âge de l'univers confirment et précisent la remarquable prédiction de Friedmann.
Le modèle d'univers en oscillation perpétuelle, avec ses cycles d'expansion - contraction, sera joliment appelé <<univers - phénix>> par Eddington [64], puis Lemaître. Il a été abandonné pour diverses raisons [65]. Beaucoup plus populaire aujourd'hui est l'idée d'univers <<inflationnaire>>, précédant la phase d'expansion de Friedmann, au cours de laquelle l'espace se serait dilaté à un taux beaucoup plus rapide que dans la période ultérieure. D'autre part, le problème de la <<création du monde>> est étroitement lié au problème non résolu de la gravité quantique [66].
C'est également dans le dernier chapitre que Friedmann mentionne l'insuffisance des équations d'Einstein pour définir la topologie globale de l'univers, et qu'en conséquence plusieurs topologies différentes peuvent être envisagées pour une même solution des équations. Ces aspects topologiques seront développés dans son second article technique, paru en 1924 dans Zeitschrift für Physik. Nous y reviendrons au [[section]]13 après avoir examiné l'oeuvre de Lemaître, car les préoccupations topologiques des deux hommes sont l'un des signes les plus profonds de leur originalité.
Friedmann publie son "opus" majeur sur la courbure de l'espace dans la revue allemande Zeitschrift für Physik [67]. Il y démontre <<l'existence possible d'univers dont la courbure spatiale est constante par rapport aux trois coordonnées spatiales mais dépend du temps, c'est-à-dire de la quatrième coordonnée (temporelle)>> et il en écrit la métrique, qui sera plus tard appelée métrique de Friedmann. Autrement dit, Friedmann franchit le pas qu'Einstein n'avait pas été prêt à faire : si l'on abandonne l'hypothèse d'un univers statique, le problème cosmologique relativiste comporte une infinité de solutions dans lesquelles la métrique varie en fonction du temps.
Friedmann discute le cas d'un univers homogène et isotrope, c'est-à-dire avec une densité de matière constante dans l'espace. Le relation entre distribution de matière et courbure, stipulée par les équations d'Einstein, impose que la courbure spatiale de l'univers est uniforme (constante en chaque point de l'espace à un instant donné). Dans ce premier article, Friedmann ne considère que le cas d'une courbure spatiale positive (le cas négatif fera l'objet de son article de 1924). Si le rayon de courbure R est indépendant du temps, démontre-t-il, les seules solutions sont les univers statiques de Einstein et de Sitter. Si R(t) dépend de la variable temporelle, il y a une infinité de modèles non statiques, en expansion monotone ou en oscillation périodique selon la valeur choisie pour la constante cosmologique l. Cette dernière, introduite par Einstein et adoptée par de Sitter pour assurer l'existence de solutions statiques, n'est plus nécessaire; comme il l'écrit, c'est <<une constante superflue du problème>>. Elle peut néanmoins être conservée, et ses diverses valeurs possibles engendrent toute une variété de modèles. Si l est positive et supérieure à une certaine valeur critique, le rayon de courbure de l'univers croît monotonement à partir d'une valeur initiale nulle; le modèle est dit monotone de première espèce. Si l est positive mais inférieure à la valeur critique, le rayon de courbure de l'univers croît monotonement à partir d'une valeur initiale non nulle; le modèle est dit monotone de seconde espèce. Enfin, si l <= 0, on obtient un modèle oscillant avec des ères alternées d'expansion et de contraction. Friedmann note que si l = 0, la période ne dépend que de la masse totale de l'univers, ce qui lui permet d'estimer numériquement le <<temps depuis la création du monde>> et obtenir une valeur <<de l'ordre de dix milliards d'années>>.
La modernité de l'article de Friedmann se voit également dans le fait que quiconque étudiant la cosmologie moderne peut reconnaître aussitôt ses principales équations [68]. Alors que les formulations des diverses métriques (celle de Sitter autant que celles de Friedmann) changeront ultérieurement pour la forme unifiée de Robertson et Walker (cf. Encadré 1), les équations différentielles qui gouvernent le développement temporel d'un espace de courbure positive constante n'ont pas changé d'un iota.
Avec son article de 1922, Friedmann introduit une révolution scientifique de même ampleur que la révolution copernicienne. Dans la cosmologie pré-copernicienne, l'espace était centré sur un lieu très particulier, la Terre. Dans la cosmologie pré-friedmannienne, le déroulement temporel de l'univers était réduit à un cas très particulier, la staticité, c'est-à-dire l'absence de toute évolution. La cosmologie friedmannienne introduit de façon irréversible l'historicité de l'univers comme espace-temps, et l'idée d'un commencement.
Mais la communauté scientifique des années 1920 n'est pas préparée à recevoir ces "faits curieux", comme les qualifie Friedmann dans son livre de vulgarisation. Au premier rang figure Einstein. Zeitschrift für Physik étant la revue de physique la plus lue de l'époque, le père de la relativité remarque l'article de Friedmann et réagit rapidement. Le 18 septembre 1922, il fait paraître dans la même revue une courte <<remarque>> [69], dans laquelle il prétend que Friedmann a fait une erreur de calcul et que les solutions à rayon variable sont incompatibles avec la relativité.
<<Dans le travail cité, les résultats concernant un univers non statique me semblent sujets à caution>>, affirme-t-il. En fait, c'est Einstein lui-même qui commet une erreur de calcul [70], mais une suite de circonstances fortuites [71] retardera de plusieurs mois la reconnaissance de cette erreur.
Le numéro de la revue Zeitschrift für Physik contenant l'objection d'Einstein parvient en Russie en octobre 1922. Friedmann et ses collègues - en particulier Frederiks - en prennent connaissance, et Friedmann décide de répondre par courrier. Il n'envoie pas sa lettre au bureau éditorial de la revue mais à Einstein, montrant ainsi un certain tact envers son prestigieux contradicteur. En fait, il est probable que Friedmann a pris connaissance de la critique d'Einstein un peu avant, ainsi qu'en témoigne le début de sa lettre: <<Cher Professeur! Selon la lettre d'un de mes amis qui est maintenant à l'étranger, j'ai eu l'honneur d'apprendre que vous avez soumis une courte note destinée à être publiée dans le volume 11 de Zeitschrift für Physik, où vous établissez que si l'on accepte les hypothèses faites dans mon article <<Sur la courbure de l'espace>>, il s'ensuit que d'après les équations d'univers que vous avez dérivées, le rayon de courbure de l'univers est une quantité indépendante du temps>>. L'ami en question est Yu. A. Krutkoff, qui va jouer pendant quelques mois le rôle de "messager" entre Einstein et Friedmann.
Krutkoff est l'un des physiciens russes les plus cultivés de son temps. Il a étudié la relativité restreinte avec Ehrenfest entre 1907 et 1912, et, en 1920, il a participé au séminaire de l'Université de Petrograd organisé par Friedmann et Frederiks, consacré à la relativité générale. Dans les nombreux agendas de notes et la correspondance que Krutkoff a laissés, nous apprenons qu'en 1922-1923 il a passé <<un an et un jour>> en Allemagne. Plus précisément, Krutkoff arrive à Berlin à la fin septembre 1922, peu après la publication de la remarque d'Einstein. Il a donc vraisemblablement informé Friedmann de la critique d'Einstein avant que la revue ne parvienne à Saint-Petersbourg. Aucune correspondance entre Krutkoff et Friedmann n'a pu toutefois être retrouvée.
Dans sa lettre à Einstein, Friedmann montre ensuite par des calculs directs que l'annulation de la divergence du tenseur impulsion-énergie [72] interdit d'obtenir un rayon de courbure constant dans le temps. <<Considérant que l'existence possible d'un univers non-statique présente un certain intérêt - écrit Friedmann -, je me permettrai de soumettre ici les calculs que j'ai effectués à votre jugement critique>>. Friedmann précise ensuite qu'il a récemment étudié <<le cas d'un univers à courbure négative constante et variable dans le temps [...]. La possibilité d'obtenir à partir de vos équations d'univers une solution à courbure négative constante est pour moi d'un intérêt exceptionnel, et je vous prie donc, bien que je vous sache très occupé, de répondre à ma lettre>>. Ce passage prouve que dès 1922, Friedmann avait découvert les solutions à courbure négative, mais celles-ci ne seront publiées que deux ans plus tard. Friedmann conclut sa lettre : <<Au cas où vous estimeriez corrects les calculs présentés dans cette lettre, je vous prie d'être assez aimable pour en informer les éditeurs de Zeitschrift für Physik; peut-être dans ce cas publierez-vous un correctif à votre note, ou donnerez-vous à cette lettre l'occasion d'être publiée>>.
Friedmann a raison de supposer qu'Einstein est <<très occupé>>. Des semaines s'écoulent sans obtenir de réponse. L'explication est simple : lorsque la lettre parvient à Berlin en décembre, Einstein a quitté la ville. Dès la fin septembre, deux semaines après avoir envoyé son commentaire sur l'article de Friedmann, lui et son épouse entreprennent un grand voyage qui les fait d'abord passer par la Suisse et la France, et le 11 octobre ils embarquent pour le Japon. Au cours de ce voyage, Einstein apprend qu'il a reçu le prix Nobel de physique. Il ne peut se présenter à Stockholm à temps pour la cérémonie de remise des prix. Ce n'est qu'en mars 1923, après être passé par la Palestine, la France et l'Espagne, qu'Einstein regagne Berlin. Il lui faut évidemment quelque temps pour trier le courrier accumulé durant son absence de près de six mois. En mai, Einstein est invité en Hollande, à l'Université de Leyde - dont il était professeur honoraire -, pour assister au dernier cours public de Lorentz. Krutkoff se trouve à Leyde au même moment. Einstein fait sa rencontre au domicile d'Ehrenfest, où il séjournait toujours quand il se rendait en Hollande. Einstein avait déjà entendu parler de Krutkoff, comme en témoigne la correspondance entre Max Born et Einstein [73].
On peut suivre les entretiens que Krutkoff a eus avec le grand physicien d'après les notes de ses agendas et les lettres qu'il a envoyées à sa soeur, Tatiana Krutkova. L'agenda du mois de mai 1923 est couvert de formules extraites de l'article de Friedmann et de calculs s'y rapportant. Dans une des lettres, Krutkoff écrit : <<Lundi 7 mai 1923, j'ai lu avec Einstein l'article de Friedmann paru dans la Zeitschrift für Physik>>. Dans une autre lettre du 18 mai : <<A cinq heures, Einstein a fait un compte-rendu de son dernier article devant Ehrenfest, Droite et un Belge ... J'ai défait Einstein dans son argumentation contre Friedmann. L'honneur de Petrograd est sauf!>>.
On ne sait si, au moment de cette entrevue, Einstein avait déjà lu la lettre que lui avait adressée Friedmann, ou bien si c'est l'entrevue avec Krutkoff qui l'a pressé de trier son courrier à son retour à Berlin. Toujours est-il que le 16 mai 1923, Einstein regagne Berlin et le 21 mai, il soumet sa seconde note [74] sur l'article de Friedmann à la Zeitschrift für Physik.
Son texte, très bref, est le suivant : <<Dans une note antérieure j'ai critiqué le travail susmentionné. Mais - comme je m'en suis convaincu à l'instigation de M. Krutkoff et grâce à une lettre de M. Friedmann - mon objection était fondée sur une erreur de calcul. Je tiens les résultats de M. Friedmann pour justes et éclairants. Ils montrent que les équations du champ admettent pour la structure de l'espace à symétrie centrale, en plus des solutions statiques, des solutions dynamiques (c'est-à-dire variant avec la coordonnée de temps).>>
Peut-on en déduire qu'Einstein admet enfin la découverte de Friedmann comme étant de nature à dessiner une nouvelle image de l'Univers? C'est peu probable, comme le montreront également ses réticences ultérieures envers le travail de Lemaître. Un article récent de D.J. Stachel [75] fait état d'une première version (non publiée) de la note, dans laquelle la dernière phrase du manuscrit <<... les équations du champ admettent [...] des solutions dynamiques [...]>> se prolongeait par <<auxquelles il est à peine possible d'attribuer une signification physique>>. Cette phrase a été - au dernier moment - biffée par Einstein. Elle est similaire à la sentence qu'il édictera plus tard, en 1927, à l'encontre du travail de Lemaître. L'attitude d'Einstein vis-à-vis du problème cosmologique traduit donc une sorte de malaise qui ne se résoudra jamais réellement [76].
En août et septembre 1923, Friedmann fait un séjour à Berlin et tente de rencontrer Einstein. Le 9 août, Krutkoff écrit à sa soeur: <<Friedmann est ici; aujourd'hui, dans quelques heures il part à Hambourg. La note d'Einstein, dans laquelle il est réhabilité grâce à mon intervention, est déjà sortie>>. Le 19 août, c'est Friedmann qui écrit à N. Malinina - sa future épouse: <<Mon voyage se déroule mal - Einstein, par exemple, a quitté Berlin pour des vacances, et je ne pourrai pas le voir>>. Le 2 septembre : <<les seules choses que j'ai à faire sont les suivantes : 1) visiter Göttingen; 2) voir Pahlen (un astronome qui a été mon collaborateur); 3) voir Mises (l'éditeur de Zeitschrift für Ang. Math.) et Einstein>>. Le 13 septembre: <<Aujourd'hui j'ai rendu visite à l'astronome Pahlen [77], un vieil ami à moi. Là, j'ai rencontré l'astronome Freundlich, une personne très intéressante, nous avons parlé de la structure de l'univers...>>.
Friedmann, Pahlen et Freundlich restent d'une certaine façon associés dans l'histoire de l'astronomie par le fait que trois cratères de la Lune portent leurs noms. Friedmann avait connu Pahlen à Saint-Petersbourg avant la première guerre mondiale, et durant la guerre ils s'étaient tous deux retrouvés à Kiev dans la même équipe d'aviation. L'autre astronome mentionné dans la lettre, Erwin Finlay Freundlich (1885-1964), avait travaillé en 1911 avec Einstein sur l'orbite de Mercure. En 1916 il avait publié à Berlin un livre de vulgarisation scientifique, Les fondements de la théorie de la gravitation d'Einstein, dont Einstein avait rédigé la préface. En 1918, il avait démissionné de son poste à Berlin pour travailler à plein temps avec Einstein [78]. Il sera plus tard le fondateur et le premier directeur de l'institut Einstein à Postdam.
Friedmann n'est pas parvenu à rencontrer Einstein en 1923, ni en avril de l'année suivante lors de son deuxième passage en Allemagne, à l'occasion de sa participation au Congrès International Technical Mechanics à Delft, en Hollande. Sa lettre du 13 septembre 1923 se poursuit par: <<...Tout le monde a été très impressionné par ma lutte avec Einstein et ma victoire finale; cela me fait plaisir, parce qu'en ce qui concerne mes articles, je pourrais maintenant les publier plus facilement>>.
En 1924 paraît le deuxième article cosmologique fondamental de Friedmann, <<Sur la possibilité d'un univers à courbure négative constante>> [79], toujours dans Zeitschrift für Physik. Nous avons vu plus haut qu'il en avait les résultats depuis deux ans.
Friedmann considère les modèles à courbure négative et démontre l'existence de solutions non statiques avec densité de matière positive, toutes caractérisées par une expansion monotone.
Tandis que dans le premier article de 1922, l'équation de la métrique pour un espace à courbure positive (D3) [cf. infra p. xx] peut sans peine être transformée par un changement de coordonnées en la forme de Robertson-Walker adoptée aujourd'hui (cf. Encadré 1), celle du second article décrivant un espace à courbure négative (équations D' et D") n'est plus du tout familière, et il n'est même guère évident que, dans ce choix particulier de coordonnées, l'espace soit vraiment à courbure constante. Friedmann a en fait utilisé une ancienne forme de la métrique d'un espace de courbure constante, donnée pour la première fois par Beltrami. La transformation de coordonnées qui transforme cette métrique en la forme unifiée de Robertson-Walker est <<hideuse>>, pour reprendre les termes mêmes de Robertson [80].
Tandis que dans l'article de 1922 Friedmann discutait dans le détail le développement temporel de ses solutions, dans l'article de 1924 il indique seulement la possibilité d'une expansion sans s'étendre davantage. Dans son importante conclusion, il préfère discuter d'un problème jusqu'ici jamais abordé en cosmologie: la topologie globale de l'espace. Pour lui, la signification physique fondamentale de ses résultats est que <<les équations d'univers à elles seules ne suffisent pas pour décider si l'univers est fini ou non>>. Friedmann doit effectivement penser, comme la plupart des physiciens de l'époque, que seuls les espaces de volume fini (telle l'hypersphère utilisée par Einstein dans son modèle de 1917) sont physiquement admissibles pour décrire l'espace réel. Jusqu'ici, les solutions cosmologiques d'Einstein et de Sitter en 1917, et celle de Friedmann en 1922, avaient une courbure positive et satisfaisaient ce critère. Avec les espaces à courbure négative, le problème est plus ardu : le prototype naturel d'un espace à courbure négative constante est un espace hyperbolique de volume infini. Mais Friedmann voit une échappatoire dans le fait que les équations d'Einstein ne suffisent pas à décider si l'espace est fini ou infini, même si la courbure est négative; il faut faire des hypothèses supplémentaires spécifiant des conditions aux limites, notamment le fait de savoir si certains points de l'espace sont identifiés entre eux ou non. Tout le problème de la topologie cosmique est ainsi déjà posé, mais Friedmann ne dispose pas des bases mathématiques suffisantes pour poursuivre la discussion : en 1924, la classification topologique des espaces riemanniens est encore inexistante.
Einstein n'aura pas de réaction publique au second article de Friedmann. Comme nous l'avons vu, ce dernier disparaît prématurément en septembre 1925, sans avoir eu la satisfaction de voir la moindre acceptation de ses idées cosmologiques. Au même moment, un autre homme de science européen revient des Etats-Unis pour enseigner à l'université de Louvain. Le belge Georges Lemaître va reprendre indépendamment les intuitions prémonitoires du savant russe, et les amplifier jusqu'à en faire la base de la théorie moderne du Big Bang.
Contrairement à Friedmann qui ne vint à l'astronomie qu'en 1921-1922, soit trois ans avant sa mort seulement, Lemaître fut durant toute sa longue vie étroitement lié à l'astronomie. Il a toujours senti l'absolue nécessité de confronter les faits d'observation et la théorie. Il sera, par exemple, beaucoup plus au courant que Friedmann du statut expérimental de la théorie de la relativité, et cela dès ses années d'apprentissage [81]. Lemaître n'en fut pas moins un remarquable mathématicien, tant sur le plan des mathématiques fondamentales, avec ses travaux sur les quaternions ou le problème de Störmer, qu'en analyse numérique [82]. Il est à noter que, contrairement à Friedmann, Lemaître n'aura aucune affinité avec l'approche axiomatique des mathématiques mise à la mode par Hilbert et l'école de Göttingen.
Georges Lemaître naît le 17 juillet 1894 à Charleroi [83]. Aîné d'une famille de la moyenne bourgeoisie, il est formé au Collège Jésuite de Charleroi et, à l'âge de 17 ans, il commence des études d'ingénieur à l'université de Louvain. En 1914, il s'engage volontairement dans l'artillerie belge ; à la fin de la guerre, il reçoit l'une des plus hautes distinctions militaires.
Revenu en 1919 à l'université, il change d'orientation en passant des études d'ingéniérie à celles, beaucoup plus abstraites, des sciences physiques et mathématiques. Il s'y révèle de première force. En 1920, il obtient son doctorat de mathématiques (correspondant aujourd'hui à la licence en sciences belge ou à la maîtrise française). Dès cette époque, Lemaître manifeste l'ouverture d'esprit et la diversité d'intérêts qui le caractériseront par la suite, puisque parallèlement à ses travaux mathématiques de haute volée, il obtient un diplôme de bachelier en philosophie thomiste. La science ne représente, en effet, pas tout pour lui. La même année 1920, Lemaître entre au séminaire de Malines, à la Maison Saint Rombaut réservée aux <<vocations tardives>>. Le 23 septembre 1923, il est ordonné prêtre par le cardinal Mercier, archevêque de Malines et Primat de Belgique. Sa formation ecclésiastique n'aura donc duré que trois années seulement, au lieu des six prescrites par les statuts canoniques.
En même temps, Lemaître prépare, seul, un mémoire sur la relativité et la gravitation pour un concours de bourses de voyage. Il est de toute évidence impressionné par la théorie d'Einstein, à cette époque pratiquement inconnue des cercles que Lemaître fréquente. En juillet 1923, il obtient une bourse du gouvernement belge lui permettant d'étudier à l'étranger. Il passe ainsi une première année à Cambridge, en Angleterre, où il apprend l'astronomie stellaire sous la direction du célèbre astrophysicien Eddington. Arthur Stanley Eddington (1882-1944) était directeur de l'Observatoire de Cambridge depuis 1914. Durant la première guerre mondiale, il avait obtenu une copie des articles publiées par Einstein à Berlin par l'intermédiaire de son collègue hollandais Wilhem de Sitter. Il avait accepté sans réserve la théorie de la relativité générale, et l'avait fait connaître en Angleterre en 1918 par un rapport à la Physical Society of London intitulé The Relativity Theory of Gravitation. Eddington avait ensuite dirigé l'expédition à l'île Principe destinée à mesurer la déflexion des rayons lumineux lors de l'éclipse de soleil de 1919. En 1920, Eddington avait rédigé un exposé de la gravitation einsteinienne à l'usage des profanes, Space, Time and Gravitation [84]ainsi qu'en 1923 l'ouvrage technique The Mathematical Theory of Relativity [85].
Lemaître a soigneusement étudié l'oeuvre d'Eddington au moment où il arrive à Cambridge, et l'année passée à ses côtés ne fera qu'augmenter son admiration pour lui [86]. La seconde année de bourse, Lemaître se rend au Cambridge américain, au Harvard College Observatory, où il travaille avec Shapley sur le problème des nébuleuses. Harlow Shapley (1885-1972) dirigeait le Harvard College Observatory depuis 1922. A l'époque, ses recherches portaient principalement sur les nuages de Magellan. Lemaître passe ensuite au Massachusetts Institute of Technology (MIT), où Edwin Hubble et Vesto Slipher travaillent. Le premier mesure les distances des nébuleuses en observant des étoiles variables de type Céphéides, le second estime leurs vitesses à partir de leur décalage spectral. Tout en suivant de près leurs travaux qui allaient fonder la cosmologie observationnelle, Lemaître entreprend une thèse de PhD sur les champs gravitationnels dans les fluides en relativité générale, un sujet que lui avait suggéré Eddington.
Le 8 juillet 1925, son séjour américain prend fin et Lemaître rejoint sa famille à Bruxelles. Il repart aussitôt à la deuxième assemblée générale de l'Union Astronomique, qui se tient à Cambridge du 14 au 22 juillet. En octobre, il est nommé chargé de cours à la faculté des sciences de Louvain. Le 19 novembre 1925, il soumet par écrit sa thèse doctorale au MIT : <<The gravitational field in a fluid sphere of uniform invariant density according to the theory of relativity>> [87]. Elle ne sera acceptée que le 15 décembre 1926, après révision.
En 1926-27, Lemaître se rend à nouveau aux Etats-Unis, au MIT, où il séjourne durant le troisième trimestre de l'année académique. De retour en Europe en juin 1927, il apprend par courrier que le MIT lui a enfin accordé le grade de doctorat (PhD) en sciences physiques (il a été dispensé de la soutenance orale). La même année, il est nommé professeur à l'université de Louvain et publie son article fondamental sur l'univers en expansion et les décalages spectraux. Il restera à ce poste jusqu'à sa retraite en 1964, interrompant parfois son enseignement pour de brefs séjours à l'étranger consacrés à des contacts et à des conférences scientifiques. Il a été choisi comme membre de l'Académie Pontificale des Sciences lors de sa création en 1936, en est devenu le président en mars 1960 et l'est resté jusqu'à sa mort, survenue à Louvain le 20 juin 1966.
En résumé, l'oeuvre cosmologique de Lemaître s'est construite en deux phases. Dans un premier temps, il retrouve indépendamment de Friedmann que les équations d'Einstein admettent des solutions cosmologiques non statiques. Simultanément, il prend en compte les observations américaines sur les vitesses des galaxies, auxquelles il donne un sens physique en les interprétant comme les indices d'un univers en expansion. Dans un second temps, Lemaître ose une hypothèse encore plus audacieuse, qui est en partie un prolongement logique de la théorie de l'univers en expansion. Si l'univers est aujourd'hui en expansion, dans le passé il a été beaucoup plus dense; un jour lointain, il a donc été condensé en un <<atome primitif>> dont les fractionnements successifs l'ont façonné tel qu'il est maintenant. Revue et corrigée au fil du temps, cette conception est devenue la théorie du Big Bang.
Reprenons maintenant les étapes de l'oeuvre de Lemaître.
Le premier résultat cosmologique notable de Lemaître date de 1925 et concerne la solution trouvée par de Sitter. En 1923, H.Weyl [88] avait noté que les particules dans l'univers de de Sitter s'éloignent avec des vitesses proportionnelles à leurs distances mutuelles, mais il n'avait pas fourni de système de coordonnées explicites pour prouver ses dires.
C'est Lemaître qui, dans deux articles de 1925 portant le même titre [89], montre comment on peut introduire de nouvelles coordonnées pour l'univers de de Sitter qui rendent la métrique non statique et conduisent à une relation linéaire entre la vitesse et la distance. Dans le premier article, Lemaître obtient explicitement la métrique pour un espace de courbure nulle, mettant en jeu un facteur d'échelle spatiale dépendant du temps de façon exponentielle [90]. Cette métrique sera utilisée vingt ans plus tard par les adversaires les plus acharnés de la théorie de l'univers en expansion, partisans du <<steady-state model>>. Dans le second article, Lemaître en déduit que la relation vitesse-distance dans l'univers de de Sitter est linéaire. C'est la première fois que la constante cosmologique se voit attribuer le rôle d'une force de <<répulsion cosmique>> (lorsqu'elle est positive), obligeant les lignes d'univers des particules à se séparer au cours du temps.
Restait à faire le lien avec les vitesses réelles des objets cosmiques. Dès 1922, dans son livre Théorie mathématique de la relativité, Arthur Eddington écrivait que <<l'un des problèmes les plus mystérieux en cosmologie sont les grandes vitesses de nombreuses nébuleuses. Leurs vitesses radiales sont de l'ordre de 600 km/s, et la majorité des nébuleuses s'éloignent du système solaire>>. En 1925, l'astronome américain Edwin Hubble [91] accomplit un pas décisif en cosmologie observationnelle, grâce à l'utilisation du grand téléscope du Mont Wilson. Il démontre que les nébuleuses spirales sont d'autres systèmes d'étoiles analogues à notre propre galaxie. Le terme de "nébuleuse" était utilisé par les astronomes depuis des siècles pour désigner les astres peu lumineux, analogues à des nuages et qui, contrairement aux comètes, ne changent ni de position ni d'apparence. Vesto Slipher avait déjà mis en évidence un décalage vers le rouge quasi-systématique des raies spectrales du rayonnement de ces galaxies. Traduits en termes d'effet Doppler-Fizeau, ces décalages impliquaient une vitesse de récession. L'effet Doppler-Fizeau permet en effet de mesurer les vitesses radiales des objets célestes par spectroscopie. Les spectres des astres (étoiles, galaxies) contiennent des raies sombres, ou raies d'absorption, qui correspondent aux rayonnement absorbés par les atomes in situ. Les raies spectrales des objets célestes sont comparées à celles des éléments chimiques correspondantes au repos (en laboratoire), et le décalage en longueur d'onde est relié à la vitesse de la source; un décalage vers le rouge, c'est-à-dire vers les plus grandes longueurs d'onde, indique que l'astre s'éloigne, un décalage vers le bleu signifie qu'il se rapproche.
Aucune interprétation théorique ne pouvait être donnée au décalage systématique vers le rouge, d'autant que l'effet n'était pas encore bien établi. Grâce à son passage au MIT, Lemaître est informé de ces résultats préliminaires, et contrairement à Friedmann qui ignorait les résultats expérimentaux, il affiche la volonté de tenir compte des données de l'observation de l'époque.
En 1927, il écrit son article fondamental <<Un univers homogène de masse constante et de rayon croissant, rendant compte de la vitesse radiale des nébuleuses extragalactiques>>. Comme son titre l'annonce clairement, il relie l'expansion de l'univers découlant des solutions cosmologiques de la relativité générale avec les observations sur la vitesse de fuite des nébuleuses extragalactiques.
Tout comme Einstein et de Sitter, Friedmann avait fait l'hypothèse que le terme de pression était nul (cf. Encadré 1). Les solutions proposées par Lemaître dans son article de 1927 incluent le terme de pression et sont donc plus générales. Lemaître reprend le dilemme entre les modèles d'univers de de Sitter et Einstein. Le modèle de de Sitter ignorait l'existence de la matière. Il faisait cependant ressortir les vitesses de récession observées des nébuleuses spirales comme simple conséquence du champ gravitationnel. La solution d'Einstein permettait la présence de matière et conduisait à une relation entre la densité de matière et le rayon de l'univers. Il ne pouvait cependant expliquer la vitesse de récession des galaxies. Lemaître cherche une solution des équations relativistes intermédiaire entre les modèles d'Einstein et de de Sitter, c'est-à-dire ayant à la fois un contenu matériel et expliquant la récession des galaxies.
Lemaître suppose que le rayon de courbure de l'univers, R, est fonction du temps t. Comme Friedmann, il trouve que R(t) augmente indéfiniment avec le temps, et il obtient des équations différentielles pour R presque identiques. La différence majeure est que Lemaître suppose la conservation de l'énergie et, comme nous l'avons dit plus haut, inclut la pression de radiation en même temps que le terme de densité de matière. Lemaître montre ainsi l'importance de cette pression de radiation dans les premiers stades de l'expansion cosmique. Il s'avèrera plus tard, dans le cadre des modèles de big bang, que l'approximation <<poussière>> p=0 n'est valable que pour les temps postérieurs de cent mille ans environ au big bang.
Le modèle auquel il aboutit décrit un univers de courbure positive en expansion monotone, à densité et pression non nulles, et qui, lorsqu'on remonte indéfiniment le temps dans le passé, s'approche de manière asymptotique de la solution statique d'Einstein. Ce modèle, dépourvu de singularité initiale au même titre que la solution monotone de seconde espèce de Friedmann, sera plus tard baptisé modèle d'Eddington-Lemaître (voir Figure 1 et Table).
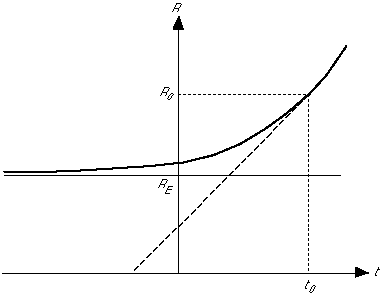
Figure 1 : Le modèle de Lemaître-Eddington.
Le rayon ![]() de
l'hypersphère d'Einstein est atteint asymptotiquement pour
de
l'hypersphère d'Einstein est atteint asymptotiquement pour
![]() . L'origine du temps
cosmique est arbitraire, le modèle ne pose donc aucun
problème d'âge.
. L'origine du temps
cosmique est arbitraire, le modèle ne pose donc aucun
problème d'âge.
Tout en donnant sa préférence à ce modèle particulier, Lemaître a néanmoins calculé l'ensemble des solutions homogènes, puisqu'il fournit les formules permettant de calculer l'évolution temporelle de tous les modèles homogènes et isotropes à courbure positive (cf. annexe, équation 11), et fait référence aux autres cas de courbure. Les archives de Lemaître à Louvain contiennent d'ailleurs un agenda rouge daté de 1927, contenant le brouillon de son article ainsi que deux diagrammes qui ne figurent pas dans la publication [92]. Ces diagrammes retracent les évolutions temporelles du facteur d'échelle spatiale en fonction de la constante cosmologique pour tous les univers de courbure positive.
L'article de 1927 de Lemaître ne fait aucune référence aux oeuvres de Friedmann, publiées pourtant dans Zeitschrift für Physik, la revue de physique théorique la plus connue à cette époque. Cette absence est d'autant plus étrange si on se rappelle les deux <<notes>> d'Einstein, publiées dans la même revue, lesquelles avaient été largement discutées dans la communauté scientifique. Une réponse possible à cette question est que Lemaître ne connaissait pas l'allemand... Le travail de Friedmann fut signalé à Lemaître par Einstein lui-même, au congrès Solvay de 1927. La référence à Friedmann apparaît ainsi dans une note du texte de 1929, La grandeur de l'espace, dans laquelle Lemaître remercie <<M. Einstein de l'amabilité qu'il a eue en me signalant l'important travail de Friedmann qui contient plusieurs des résultats contenus dans ma note Un univers homogène...>>. La référence figure également dans la traduction anglaise de l'article de Lemaître [93], publiée en mars 1931 dans Monthly Notices of the Royal Astronomical Society sous l'égide d'Eddington : <<Les équations de l'univers de rayon variable et de masse constante ont été pleinement discutées sans référence aux vitesse de récession des nébuleuses par A.Friedmann "Uber die Krummung der Raumes", Z. f. Phys. 10, 377, 1922; voir aussi A.Einstein, Z. f. Phys. 11, 326, 1922 et 16, 228, 1923. L'univers de rayon variable a été étudié indépendamment par I.C.Tolman dans P.N.A.S. 16, 320, 1930>>.
L'intérêt exceptionnel du travail de Lemaître est d'introduire pour la première fois l'idée que les vitesses de récession des nébuleuses extragalactiques sont la conséquence cosmique de l'expansion de l'univers dans le cadre de la relativité générale. Lemaître n'a donc pas seulement trouvé l'expansion (corrélativement mais indépendamment de Friedmann) comme solution des équations relativistes, il est le premier à affirmer qu'elle est la bonne solution, puisqu'elle repose sur l'analyse des observations.
<<Utilisant les 42 nébuleuses extra-galactiques figurant dans les listes de Hubble et de Strömberg, et tenant compte de la vitesse propre du Soleil, on trouve une distance moyenne de 0,95 millions de parsecs et une vitesse radiale de 600 km/s, soit 625 km/s à 106 parsecs>>, écrit-il. Lemaître annonce clairement la relation de proportionnalité entre la vitesse de fuite et la distance, cette loi que Hubble ne publiera que deux ans plus tard avec des chiffres quasiment identiques, et dont l'attribution lui reviendra au regard de l'histoire. La découverte devrait pour le moins être attribuée en partie à Lemaître; il est vrai que dans la version anglaise de l'article de Lemaître, le calcul de cette loi de proportionnalité n'a pas été traduit!
Malheureusement, l'article du jeune savant belge n'est pas plus apprécié que ne l'avaient été ceux de son prédécesseur russe. Du 24 au 29 octobre 1927, a lieu à Bruxelles le Cinquième Congrès Solvay de Physique, l'un des grands rendez-vous de la science mondiale. Le Congrès Solvay est consacré à la nouvelle discipline de la mécanique quantique, dont les problèmes perturbent de nombreux physiciens. Parmi eux, Einstein. Pour Lemaître, c'est l'occasion de parler au père de la relativité. Il a lui-même relaté plus tard cette rencontre : <<En se promenant dans les allées du parc Léopold, [Einstein] me parla d'un article, peu remarqué, que j'avais écrit l'année précédente sur l'expansion de l'univers et qu'un ami lui avait fait lire. Après quelques remarques techniques favorables, il conclut en disant que du point de vue physique cela lui paraissait tout à fait abominable>>. Le lecteur remarquera ici la ressemblance avec la phrase finale de la seconde note sur l'article de Friedmann, que, comme nous l'avons vu, d'Einstein avait supprimée dans la publication finale. Lemaître poursuit : <<Comme je cherchais à prolonger la conversation, Auguste Piccard qui l'accompagnait, m'invita à monter en taxi avec Einstein qui devait visiter son laboratoire à l'Université de Bruxelles. Dans le taxi, je parlai des vitesses des nébuleuses et j'eus l'impression qu'Einstein n'était guère au courant des faits astronomiques. A l'université, tout se passa en allemand>>. Dans ses savoureuses notes ajoutées à l'article d'Odon Godart (op. cit.), André Deprit (ancien élève de Lemaître) donne une version plus pittoresque et légèrement différente de cette rencontre. Il affirme notamment que Lemaître ne connaissait pas l'allemand, ce qui peut expliquer le fait que Lemaître n'ait pas cité le travail antérieur de Friedmann dans son article de 1927.
Lemaître a envoyé sa note à Eddington mais n'a pas reçu de réponse; son ancien directeur de thèse a classé le manuscrit sans le lire vraiment. En juillet 1928, Lemaître se rend à Leyde, où de Sitter préside la troisième assemblée de l'Union Astronomique Internationale, mais il ne le rencontre pas. L'heure du Big Bang n'est manifestement pas encore venue.
Une nouvelle occasion se présente en février 1930 qui, cette fois, sera décisive. En janvier, à Londres, une réunion de la Royal Astronomical Society est le théâtre d'une discussion entre Eddington et de Sitter. Ils ne savent comment interpréter les données sur les galaxies. Eddington suggère que le problème pourrait venir du fait que seuls des modèles d'univers statiques aient été considérés.
Ayant lu un rapport de la réunion de Londres [94], Lemaître comprend qu'Eddington et de Sitter se posent un problème qu'il a résolu deux ans plus tôt. Il écrit à Eddington pour lui rappeler son envoi de 1927 et le prier d'en transmettre une copie à de Sitter. Cette fois, Eddington réagit. L'ancien mentor de Lemaître est l'une des plus puissantes figures de la science à l'époque, et il va jouer un rôle clé dans l'acceptation de l'hypothèse de Lemaître. Il envoie la note à de Sitter, en Hollande, et à Shapley, aux États-Unis. Eddington est quelque peu embarrassé. Il accompagne l'envoi à de Sitter par le commentaire suivant: <<C'est le compte-rendu de vos interventions et des miennes à la Royal Astronomical Society qui ont incité Lemaître à m'écrire. A ce moment, un de mes étudiants-chercheurs, Mc Vittie et moi-même nous tracassions pour le problème et nous avions fait de considérables progrès; ce fut dès lors un choc pour nous, de découvrir que ce travail avait été fait beaucoup plus complètement par Lemaître (un choc atténué, en ce qui me concerne, par le fait que Lemaître fut un de mes élèves)>>.
De Sitter répond à Lemaître très favorablement (cf. la lettre de de Sitter à Lemaître du 25 mars 1930, en annexe). De son côté, Eddington a remodelé son projet de communication à la réunion suivante de la Royal Astronomical Society en mai (qui portait sur la stabilité de l'univers d'Einstein), pour faire une présentation favorable du modèle d'Univers en expansion de Lemaître [95]. Eddington publie ensuite un article important [96] dans lequel il prouve l'instabilité du modèle statique d'Einstein et discute le modèle d'univers en expansion de Lemaître - qui restera sous le nom de modèle d'Eddington-Lemaître. Enfin, Eddington fait réaliser une traduction de l'article de Lemaître de 1927 pour les comptes-rendus de la Royal Astronomical Society (cf. supra).
Dès lors, l'Univers en expansion est en passe de devenir le nouveau paradigme cosmologique. L'idée était dans l'air du temps. Weyl, Lemaître et d'autres [97] avaient d'une part tenté de relier à la solution de de Sitter les vitesses radiales positives observées. En se fondant sur ses propres observations et sur celles de Slipher achevées en 1926, Hubble avait d'autre part établi en 1929 que la vitesse de récession v de n'importe quelle galaxie est proportionnelle à sa distance r. Il donnait ainsi la <<loi de Hubble>> selon laquelle v = Hr, où H est appelée <<constante de Hubble>> car sa valeur est constante pour toute galaxie et indépendante de la distance.
Nous avons vu que dans son article de 1927, Lemaître avait déjà trouvé cette loi et fixé la valeur de la constante (que l'on n'appelait pas encore constante de Hubble, et pour cause) à 630 km/s. Lemaître avait donc prédit ce que Hubble était en train de patiemment redécouvrir, et la fameuse loi devrait pour le moins porter leurs deux noms. D'autant que Hubble, auquel on attribue le plus souvent la paternité de l'expansion de l'univers, n'admit qu'avec beaucoup de réticence que la récession des galaxies puisse résulter de l'expansion de l'espace.
Il n'y avait pourtant pas d'autre explication cohérente, et Einstein lui-même finit par l'accepter. Mais au moment même où Eddington et Einstein le rejoignent dans sa vision d'un univers dynamique, Lemaître est déjà plus loin. Au lieu de considérer le monde statique d'Einstein comme stade initial à partir duquel commence le modèle dynamique, Lemaître préfère penser que l'univers a commencé son expansion à partir d'un état initial singulier, l'atome primitif. Entre eux va ainsi se creuser le fossé d'une autre controverse, qui ne se résoudra pas de leur vivant : celle de la naissance même de l'univers.
Cette idée capitale, Lemaître la développe dans le texte <<L'expansion de l'espace>>, publié dans la Revue des Questions Scientifiques en novembre 1931. C'est la version simplifiée d'un travail publié en mars sous forme technique et en anglais dans les Monthly Notices [98], juste à la suite de la traduction de son article de 1927.
Le style de Lemaître contraste absolument avec celui de Friedmann, tant sur le fond que sur la forme. Sur le fond, autant l'approche de Friedmann était axiomatique, autant celle de Lemaître - lui-même remarquable mathématicien - est physique. Quant à la forme, très littéraire (adaptée à celle des conférences publiques que Lemaître donnait fréquemment), c'est un modèle de rigueur et de lyrisme mêlés, lisible par presque tous et qui témoigne des années d'études de Lemaître en humanités gréco-latines. Comme le signale André Deprit [99], le jeune Lemaître avait suivi en 1908-1909 une classe de poésie sous la direction de Franz Charlier; ce dernier s'était fait une réputation de critique impitoyable en matière de style.
On peut se demander si la qualité de forme de son oeuvre n'a pas nui à la crédibilité de son fond, du moins dans les pays anglo-saxons peu habitués à cette façon fleurie d'écrire la science. Aujourd'hui encore, bien des scientifiques ont vite fait de taxer péjorativement de <<vulgarisation>> un texte haussant la qualité de la forme au même niveau que celle du fond.
Le fond, précisément, est d'une richesse inouïe. Là encore, Lemaître part des données expérimentales : l'observation des décalages vers le rouge des nébuleuses lointaines traduit l'expansion de l'univers, mais l'existence même de ces nébuleuses impose que, dans son passé, l'univers ait aussi connu des processus de contraction qui leur ont donné naissance. Pour Lemaître, expansion de l'espace et contraction de la matière sont les manifestations de déséquilibres entre deux forces cosmiques opposées : la gravitation, attractive, et celle décrite par la constante cosmologique, répulsive.
Par ailleurs, le résultat des observations impose une durée très restreinte pour l'évolution du monde et implique la nécessité d'une cosmogonie rapide. Selon Hubble en effet, le taux d'expansion est égal à 540 km/s/Mpc. Avec un taux d'expansion aussi rapide et en l'absence de constante cosmologique, l'univers actuel devrait avoir quelques 2 milliards d'années d'existence. Or on sait déjà, par l'étude des éléments radioactifs, que l'âge de la Terre est d'au moins 4 milliards d'années. Il est évidemment impossible que la Terre soit plus vieille que l'univers. Lemaître a donc doublement besoin de la constante cosmologique reniée par Einstein, à la fois pour rendre l'âge de l'univers compatible avec celui de la Terre, et pour laisser le temps aux condensations galactiques de se former.
Le modèle de Lemaître (cf. Fig. 2) divise l'évolution de l'univers en trois phases distinctes : deux expansions rapides séparées par une période de ralentissement. La première phase est une expansion de type explosif, issue de la désintégration radioactive d'un atome-univers. Pour cette phase, Lemaître utilise l'image du feu d'artifice qui, si elle est poétique, n'en est pas moins pédagogiquement contestable : elle a été source d'un malentendu constamment reconduit par la vulgarisation, présentant le Big Bang comme une explosion ponctuelle de matière dans un espace extérieur. La seconde phase correspond à un quasi-équilibre entre la densité de matière et la constante comologique, résultant en un rayon pratiquement constant durant une période dite de stagnation; les effets attractifs de la gravitation étant prépondérants à petite échelle, c'est au cours de cette phase que se forment les fluctuations de densité, lesquelles se condensent ultérieurement pour donner naissance aux grandes structures de l'univers, avec ses étoiles groupées en galaxies et ses galaxies en amas. La formation des condensations locales dérange les conditions d'équilibre, ce qui rend prééminente la contante cosmologique et déclenche la reprise de l'expansion. C'est la troisième phase, celle que nous observons aujourd'hui.
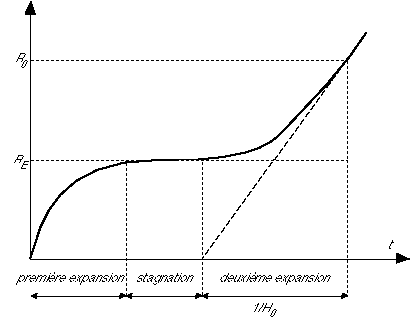
FIGURE 2 : L'Univers "hésitant" de Lemaître
Techniquement, la solution s'obtient à partir des équations
relativistes en supposant l'espace à courbure positive et une constante
cosmologique légèrement supérieure à la valeur
einsteinienne
![]() ,
où
,
où
![]() est
le rayon d'équilibre de l'univers d'Einstein. La durée de la
période de stagnation varie beaucoup avec le choix de l,
elle est d'autant plus longue que l est proche de
est
le rayon d'équilibre de l'univers d'Einstein. La durée de la
période de stagnation varie beaucoup avec le choix de l,
elle est d'autant plus longue que l est proche de
![]() .
Pour cette raison, le modèle est parfois appelé "univers
hésitant".
.
Pour cette raison, le modèle est parfois appelé "univers
hésitant".
Dans cet enchaînement de phases, la plus originale est la première car elle pose la question de l'origine singulière de l'univers, que Lemaître baptise pour la première fois du nom d'atome primitif. Là encore, la terminologie est spectaculaire, mais pédagogiquement discutable. En un sens elle est faible car un atome est un système physique localisé dans l'espace ; elle est bien plus heureuse si l'on prend a-tome au sens étymologique : qu'on ne peut séparer ; elle signifie alors que l'univers est unique et inséparable, sans aucun parti-pris de localisation.
Le raisonnement de Lemaître s'appuie sur la volonté d'utiliser les nouvelles connaissances de la physique atomique et de lier les nébuleuses aux atomes : <<une cosmogonie vraiment complète devrait expliquer les atomes comme les soleils>>, écrit-il. Prenant appui sur les phénomènes radioactifs, Lemaître conçoit l'univers primitif comme un quantum unique, dont la désintégration a donné naissance à tous les composants actuels de l'univers. A son modèle précédent, à évolution lente, Lemaître oppose désormais une cosmologie rapide, avec une origine explosive, qui, partant du plus simple, engendre le complexe.
Personne n'a pensé et défendu avec une telle force cette conception du commencement du monde : <<Nous pouvons concevoir que l'espace a commencé avec l'atome primitif et que le commencement de l'espace a marqué le commencement du temps>>. Il est toutefois important de souligner, eu égard aux tempêtes de protestations ultérieurement soulevées par les termes de genèse et de création, combien la conception que Lemaître se faisait de la singularité initiale n'a jamais reposé sur une confusion scientifico-religieuse, mais sur une conception naturelle de l'origine s'opposant à une création surnaturelle [100].
Lorsqu'Einstein doit admettre la réalité expérimentale de l'expansion, il regrette amèrement d'avoir introduit la constante cosmologique, et il ne se départira plus d'un certain sentiment d'échec face au problème cosmologique - d'autant qu'en 1930, Arthur Eddington démontrait l'instabilité de son modèle statique.
En 1931, dans son article <<Sur le problème cosmologique en théorie de la relativité générale>> [101], Einstein reconnaît définitivement l'importance des travaux de Friedmann pour la description de l'univers suite aux observations de Hubble, mais il ne cite pas Lemaître. En 1932, les deux promoteurs de l'univers statique, Einstein et de Sitter, unissent leurs efforts pour <<rattraper le coup>>. Ils publient un article d'une page [102] où ils font valoir qu'un univers en expansion est aussi possible sans introduire de courbure spatiale, ni de pression, ni de constante cosmologique. Il suffit pour cela que la densité de matière soit exactement égale à la valeur critique qui sépare les cas elliptique (courbure positive) et hyperbolique (courbure négative).
Cet article, il faut le reconnaître, est un singulier appauvrissement des calculs effectués précédemment par Friedmann, Lemaître et Robertson. Friedmann et Lemaître avaient déjà montré que des univers en expansion étaient possibles, avec ou sans constante cosmologique, et une courbure spatiale négative. Le cas à courbure nulle k=0 avait été décrit par Robertson [103] en 1929 dans le cadre des métriques spatialement homogènes et isotropes. Or, Einstein et de Sitter ne font référence ni à Friedmann ni à Lemaître, mais à Heckman [104].
Que d'efforts de leur part pour retrouver la solution la plus simple ! Bien leur en prend cependant au regard de l'histoire. Leur article tombe au bon moment et a deux prestigieux signataires; c'est donc lui qui va rester, et longtemps occulter la profonde richesse des solutions de Friedmann et Lemaître - à tel point qu'aujourd'hui encore, lorsqu'on lit dans la presse scientifique que le modèle de Big Bang est menacé par de nouvelles observations sur l'âge des étoiles, les auteurs se réfèrent uniquement à la solution très simplifiée d'Einstein-de Sitter.
La balance précise entre la densité réelle et la densité critique est encore l'objet d'un débat controversé. Les modèles d'inflation développés à partir des années 1980 suggèrent un univers presque <<plat>>, c'est-à-dire, en l'absence de constante cosmologique, une densité de matière très proche de la densité critique; en revanche, les observations astronomiques actuelles favorisent un univers de densité nettement sous-critique (donc hyperbolique), avec peut-être une constante cosmologique non nulle [105].
Notons par ailleurs que la valeur de la constante de Hubble H0, déterminée expérimentalement par l'astronome américain, était fausse, plus grande d'un ordre de grandeur que la valeur mesurée aujourd'hui. L'erreur de Hubble venait d'une estimation erronée des distances aux autres galaxies. Les valeurs de ces distances seront reconsidérées par Walter Baade en 1952 et par Allan Sandage en 1958, et conduiront à une nouvelle valeur beaucoup plus basse de H0. Ce fait a joué un rôle retardateur dans l'acceptation du concept de Big Bang. En effet, à partir de la valeur initiale proposée par Hubble, l'âge de l'univers, calculé dans le cas d'une constante cosmologique nulle, était beaucoup plus petit que l'âge de la terre (cf. supra). L'hypothèse de l'expansion de l'univers n'y trouvait guère de crédibilité, à moins d'adhérer au modèle avec constante cosmologique de Lemaître.
Il est remarquable qu'aujourd'hui encore, des adversaires acharnés du Big Bang - souvent pour des raisons extra scientifiques - se focalisent sur une possible incompatibilité entre l'âge de l'univers théorique (calculé à partir de la constante de Hubble) et l'âge des plus vieux objets de l'univers (non plus la terre, mais les plus vieilles étoiles) [106]. Dans cette confrontation, certaines valeurs des paramètres dont dépend l'âge théorique de l'univers - par exemple le rapport de la densité réelle à la <<densité critique>> et la constante cosmologique, sont trop vite oubliés. Maints cosmologistes ayant longtemps supposé que la densité était égale à la densité critique, pour des raisons diverses mêlant l'histoire (le modèle d'Einstein - de Sitter servant de référence), la simplicité (le calcul étant plus facile) et la mode (la jolie théorie de l'inflation permettant de justifier l'assertion), les adversaires du Big Bang ont eu beau jeu d'annoncer à grand fracas la mort du modèle, relayés aussitôt par une presse avide de nouvelles sensationnelles. Il est en effet plus intéressant d'annoncer au grand public qu'une théorie célèbre (bien qu'incomprise) est morte, plutôt que d'avouer qu'elle résiste bien aux observations à l'intérieur de certaines <<barres d'erreur>>. Combien n'a-t-on pas vu d'articles dans la presse de vulgarisation scientifique faisant leur titre sur la <<mort du Big Bang>>! Or, si le modèle ultra-simplifié d'Einstein-de Sitter, avec la densité critique et la constante cosmologique nulle, semble effectivement écarté par les observations, les modèles de Big Bang pour des valeurs de la densité cinq ou dix fois inférieures à la valeur critique - compatibles avec ce qui est précisément observé - résistent parfaitement à la confrontation des âges...
A l'instar de nombreux autres physiciens, Lemaître est assez impressionné par la nouvelle mécanique quantique. En raison de cet intérêt, il accepte l'invitation de la British Association for Science de Londres à participer à son colloque annuel, consacré aux relations entre <<l'univers physique et la vie de l'esprit>>. Lemaître y exprime l'idée d'une création singulière de l'univers en expansion et esquisse le modèle de l'atome primitif. Comme nous l'avons dit plus haut, la création singulière de l'univers avait été brièvement abordée par Friedmann, mais totalement ignorée par la communauté scientifique.
Dans la foulée, il publie une lettre dans l'édition du 9 mai 1931 de la revue scientifique britannique Nature. Ce court texte (cf. Annexe infra, p. xxx) est considéré comme la <<charte>> de la théorie du Big Bang. La nouveauté radicale introduite par Lemaître consiste à lier la structure de l'univers à grande échelle à la nature intime des atomes, autrement dit lier la physique de l'infiniment grand à celle de l'infiniment petit. Lemaître utilise le terme <<quantum unique>> et non celui d'atome primitif. Il prend bien garde de souligner qu'à ce stade, les lois de la physique telle que nous la connaissons n'ont plus de sens, car au tout début de l'espace-temps, les notions d'espace et de temps ne sont pas définies. C'est la frontière de la science telle que Lemaître la conçoit, et rien n'indique aujourd'hui que cette frontière - appelée ère de Planck et correspondant à un temps de 10-43 seconde - puisse être franchie.
A la suite d'Eddington [107], Lemaître suppose que le temps et sa flèche sont reliés à la croissance de l'entropie. Dans le sens des temps croissants, l'univers court à sa fin qui serait un état d'entropie infinie, c'est-à-dire de désorganisation complète. Dans la direction du passé, l'univers procéderait d'un état d'entropie nulle. Eddington s'était demandé si l'instant d'entropie nulle pouvait marquer le commencement du monde, une notion qu'il avait des raisons personnelles de repousser. Lemaître fait remarquer que l'entropie est une mesure du temps propre et non pas du temps-coordonnée; dès lors, Eddington a tort de croire que l'instant d'entropie minimale sépare l'avant-création de l'après-création sur un axe de temps universel. Il faut le voir au contraire comme une singularité essentielle où les notions d'espace et de temps même perdent leur sens. Pour qu'il y ait espace-temps au sens de la relativité générale, il faut un tenseur d'énergie matérielle, en vertu de l'identification de la géométrie à la matière. La matière dans un état non décomposé (d'entropie nulle) constitue une singularité du tenseur de matière dans le membre de droite des équations, ce qui revient à une singularité dans le tenseur de courbure au membre de gauche. Il n'y a pas de temps ni d'espace préalables à la condensation d'entropie nulle. C'est la singularité intiale qui crée l'espace-temps. Ainsi, la pluralité et la diversité du monde physique paraissent provenir de <<quelque chose>> de physique, coïncidant avec la singularité R=0 de certains modèles cosmologiques relativistes. L'atome-univers a explosé et la pluralité a surgi. L'entropie est devenue non nulle, le temps et sa flèche sont apparus également. Cette idée de Lemaître correspond bien à ce que l'on appelle aujourd'hui la cosmologie quantique.
Dans la version dactylographiée de l'article de Lemaître, conservée aux Archives Lemaître à Louvain, figure un dernier paragraphe très bref, vraisemblablement biffé par la main de Lemaître lui-même et qui, donc, n'a jamais été publié. Lemaître concluait ainsi sa lettre à Nature: <<Je pense que quiconque croit à un être suprême soutenant chaque être et chaque acte, croit aussi que Dieu est essentiellement caché, et peut se réjouir de voir comment la physique actuelle fournit un voile cachant la création>>. Lemaître conservera toute sa vie cette conception du Dieu suprême et inaccessible dont parle le prophète Isaïe, conception lui permettant notamment de garder l'origine naturelle du monde dans les strictes limites de la physique, sans la mélanger à une création surnaturelle [108]. Il n'est pas inutile de souligner cette rigueur théologique de Lemaître, lorsqu'aujourd'hui des cosmologistes américains, après avoir détecté expérimentalement les inhomogénéités du fond diffus cosmologique, osent déclarer qu'ils ont vu <<le visage de Dieu>> !
Lemaître donne à sa cosmologie une version plus structurée
en 1933, publiée en français dans les Annales de la
Société Scientifique de Bruxelles [109]. Dans ce très remarquable texte,
lui aussi méconnu, on trouve maints trésors additionnels. Ainsi,
Lemaître démontre pour la première fois que la
singularité apparente de la solution de Schwarzschild n'est qu'une
singularité fictive, résultant d'un mauvais choix des
coordonnées. On se souvient que dès 1917, Karl Schwarzschild
découvrait la métrique d'espace-temps décrivant le champ
gravitationnel statique engendré par une masse sphérique sans
rotation, dans le vide. Cette solution devenait singulière (en ce sens
que certaines coordonnées d'espace-temps devenaient infinies) pour une
valeur non nulle du rayon, appelée rayon critique
![]() (où M est la masse, G la constante de gravitation et
c la vitesse de la lumière). Pour que ce rayon pût
être physiquement atteint, il fallait envisager un effondrement
gravitationnel de la matière conduisant à des configurations
extrêmement compactes. Ce rayon était celui déjà
calculé au XVIIIe siècle par Laplace et Michell pour
prédire l'existence d'astres invisibles, dans le contexte de la
théorie newtonienne de l'attraction universelle. Ces infinis
relativistes firent horreur à nombre de physiciens [110]. Eddington, en particulier, qualifia le
rayon critique de <<cercle magique à l'intérieur duquel
aucune mesure ne peut nous mener>>, et dénia toute pertinence
physique au concept d'effondrement gravitationnel.
(où M est la masse, G la constante de gravitation et
c la vitesse de la lumière). Pour que ce rayon pût
être physiquement atteint, il fallait envisager un effondrement
gravitationnel de la matière conduisant à des configurations
extrêmement compactes. Ce rayon était celui déjà
calculé au XVIIIe siècle par Laplace et Michell pour
prédire l'existence d'astres invisibles, dans le contexte de la
théorie newtonienne de l'attraction universelle. Ces infinis
relativistes firent horreur à nombre de physiciens [110]. Eddington, en particulier, qualifia le
rayon critique de <<cercle magique à l'intérieur duquel
aucune mesure ne peut nous mener>>, et dénia toute pertinence
physique au concept d'effondrement gravitationnel.
Dans son article de 1933, Lemaître est le premier à reconnaître que la surface du trou noir n'est pas une vraie singularité, et que si des infinis y apparaissent, c'est en raison d'un mauvais choix du système de coordonnées. Pour prouver ses dires, il construit un système de coordonnées équivalent, où ces infinis disparaissent. Malheureusement, son argumentation, perdue dans un article au contexte cosmologique plus général au lieu de faire l'objet d'une publication séparée en anglais, passe inaperçue. Le développement de la théorie relativiste du trou noir restera bloqué pendant trente ans. Le caractère artificiel de la singularité de Schwarzschild ne sera redécouvert que dans les années 1960, date à partir de laquelle les fascinants modèles relativistes de trous noirs prendront leur envol. [111]
Dans le même article, Lemaître traite brillamment le problème de <<l'évanouissement de l'espace>>, à savoir l'annulation du rayon de l'espace à la singularité cosmique. Sa motivation est de discuter la plausibilité de la solution cycloïdale proposée par Friedmann, dans laquelle l'univers fermé se dilate et se contracte successivement un grand nombre de fois : <<l'univers-phénix>>. Pour cela, il faut examiner si la solution fermée peut être mathématiquement prolongée au-delà des singularités initiale et finale, autrement dit <<s'il y a moyen d'émousser la pointe de la cycloïde>>. Lemaître esquisse alors une démonstration capitale, selon laquelle les singularités cosmologiques sont une conséquence inéluctable de la relativité générale moyennant des hypothèses raisonnables. Il démontre notamment que ni une pression non nulle, ni une anisotropie de l'espace ne peuvent empêcher l'occurrence d'une singularité. Il anticipe ainsi les <<théorèmes sur les singularités>>, redémontrés de façon plus générale dans les années 1960 et qui rendront célèbres leurs auteurs, S. Hawking et R. Penrose [112]. Lemaître en conclut que le zéro de l'espace doit être traité comme un réel commencement, en ce sens que toute structure astronomique d'une existence antérieure y aurait été complètement détruite. Il faut donc abandonner les solutions d'univers cycloïdal, qui <<avaient un charme poétique incontestable et faisaient penser au phénix de la légende>>.
En août 1932, quand il embarque pour la deuxième fois sur un bateau à destination de l'Amérique, Lemaître est précédé d'une réputation bien établie. Sa lettre à Nature l'a révélé au monde de la presse (la situation n'a guère changé aujourd'hui; il semblerait qu'une publication dans Nature constitue un passage obligé pour qu'une reconnaissance scientifique internationale puisse s'instaurer, quelle que soit la qualité des travaux publiés par ailleurs). Le New York Times titre un article le 19 mai où l'on voit les dangers de la terminologie de Lemaître : <<Lemaître suggère qu'un grand atome unique contenant toute l'énergie est à l'origine de l'Univers>>.
Le monde occidental traverse les affres de la grande dépression. Les médias tentent de remonter le moral de leurs lecteurs par des reportages excitants, parfois exagérés, sur les découvertes scientifiques spectaculaires. Lemaître devient une petite célébrité. Le Times ajoute que Lemaître est <<l'un des meilleurs physiciens mathématiciens vivants [...] . Son Univers en expansion est si populaire que le modèle statique d'Einstein paraît aussi démodé qu'un fiacre>>. Ces divagations médiatiques ne doivent guère plaire à Einstein, mais il n'en tiendra pas rigueur à Lemaître. En fait, Einstein commence à réaliser qu'il a rejeté un peu vite les idées du jeune prêtre.
La rencontre entre Lemaître et Einstein à Pasadena (Californie), en 1932, est plus réussie que la précédente rencontre à Bruxelles, en 1927 . A cette époque, Einstein songe à quitter l'Allemagne pour émigrer aux États-Unis. Le roi Albert de Belgique et la reine Elisabeth avaient sympathisé avec Einstein, et le nom de Lemaître associé à son idée d'univers en expansion avait parfois été mentionné au cours des conversations entre le physicien et le le couple royal. Ainsi, à Pasadena, Einstein ne rencontre plus un quelconque jeune scientifique inconnu, mais l'homme dont les idées nouvelles font beaucoup parler. Einstein admet la réalité de l'expansion comme conséquence de la relativité générale, à travers le modèle cosmologique de Lemaître qui est en mesure de prédire la loi de Hubble. Einstein préfère ne pas discuter de l'hypothèse de l'atome primitif, car il soupçonne le prêtre belge de ne pas être scientifiquement objectif sur cette question [113]. Il la juge <<inspirée par le dogme chrétien de la création, et injustifiée sur le plan de la physique>> [114]. La conversation est donc consacrée à la constante cosmologique. La situation doit paraître embrouillée aux yeux d'Einstein. En effet, après des années de réticence à l'égard des solutions dynamiques, Einstein a fini par céder aux arguments de Friedmann et par renier la constante cosmologique (cf. supra son article avec de Sitter). Lemaître va plus loin que Friedmann, et soutient au contraire qu'il faut conserver cette constante. Si Lemaître tenait tant à ce facteur, nous l'avons vu, c'est notamment parce que les modèles dynamiques à constante cosmologique nulle produisaient un univers trop jeune.
Les échanges, verbaux ou épistolaires, entre Einstein et Lemaître, ne manquent pas de sel. Ils ont été relatés de façon pittoresque et pleine de chaleur humaine par Lemaître lui-même, dans un texte lu à la radio nationale belge le 27 avril 1957 à l'occasion du deuxième anniversaire de la mort d'Einstein [115]. Il y raconte notamment que les journalistes qui suivaient leur conversations de Pasadena parlaient d'un <<little lamb>>, c'est-à-dire d'un <<petit agneau>>, qui les suivait partout. Dans l'article original d'Einstein, la constante cosmologique était en effet représentée par la lettre grecque l minuscule, en anglais <<little lambda>>. André Deprit [116] ajoute que Lemaître n'avait pas saisi la plaisanterie : les journalistes se référaient à une comptine bien connue dans les écoles maternelles américaines...
<<Pas plus que d'autres>>, dit Lemaître dans le même article, <<sur des sujets qui lui tenaient bien plus à coeur, [...] je n'ai pu le convaincre ni, je dois l'avouer, saisir sa pensée d'une façon bien précise>>. On peut ajouter que, réciproquement, le père de la relativité n'a jamais vraiment saisi la pensée cosmologique de Lemaître. Le physicien allemand ne cesse de regretter le caractère superflu et abominable de la constante cosmologique, tandis que le prêtre belge lui répète sans relâche qu'il a eu au contraire une idée de génie <<sans le savoir>>, parce que la constante cosmologique est indispensable pour assurer l'adéquation des modèles relativistes aux observations. Lemaître ne parviendra pas à le convaincre, comme en témoigne la correspondance de 1947 entre les deux hommes (cf. Annexe, page xxx). Notons qu'après une période d'abandon de la constante cosmologique, disons entre 1945 et 1990, qui ne fait que traduire l'influence prédominante d'Einstein, la tendance revient aujourd'hui à considérer la constante cosmologique à la fois comme une nécessité logique et comme une nécessité observationnelle [117].
L'idée de l'atome primitif est abordée devant Einstein, en janvier 1933. A la fin d'un exposé de Lemaître à l'Observatoire du Mont Wilson, en Californie, Einstein se lève, applaudit et lance qu'il s'agit là de la plus belle et la plus satisfaisante de toutes les explications de la création qu'il ait jamais entendues. Einstein et Lemaître se retrouvent la même année en mai, à Bruxelles. Pour aider Einstein en difficulté, le prêtre belge organise en effet, avec l'appui de la fondation Franqui, une série de conférences scientifiques animées par le père de la relativité. Ce dernier était arrivé à Anvers quelques semaines auparavant et avait appris l'accession de Hitler au pouvoir. Il avait renoncé à sa nationalité allemande en remettant son passeport à l'Ambassade d'Allemagne à Bruxelles, et avait démissionné de ses fonctions à l'Académie de Prusse et à l'Université de Berlin. Soutenu notamment par la reine Elisabeth de Belgique, il s'était installé provisoirement dans une villa à De Haan (Le Coq), où Lemaître était allé lui rendre visite pour lui faire part de la proposition de la fondation Franqui.
Les conférences d'Einstein ont lieu à la Fondation universitaire de Bruxelles, entourées de strictes mesures de sécurité. A l'avant-dernier séminaire, Einstein annonce sans préavis que le prochain et dernier séminaire serait animé par Lemaître <<qui a des choses intéressantes à nous dire>>. Quatre jours plus tard, Lemaître expose ses idées et est interrompu plusieurs fois par Einstein s'exclamant <<Très joli, très, très joli!>>. Einstein manifestera encore son estime envers son confrère belge en soutenant sa candidature à l'important prix Franqui, qui sera effectivement attribué à Lemaître en mars 1934.
Lemaître veut donner une base expérimentale à son hypothèse de l'atome primitif, et croit trouver dans les rayons cosmiques la manifestation de la fragmentation initiale. Il approfondit la question avec des collaborateurs tels que Odon Godart et Manuel Sandoval Vallarta (1899-1977). Lemaître avait rencontré ce dernier lors de son séjour à Harvard en 1924 et s'était lié d'amitié avec lui. L'échec de leur explication ne va pas favoriser la crédibilité du modèle de l'atome primitif.
De plus, la guerre de 39-45 coupe le chanoine Lemaître de toute relation internationale. A la sortie de la guerre, il a perdu le contact avec le monde scientifique international.
<<L'hypothèse de l'atome primitif>> est le texte d'une conférence que Lemaître donne à la session annuelle de la Société helvétique des sciences naturelles à Fribourg en septembre 1945, et publiée la même année dans les actes de cette société. Sous ce même titre figurent plusieurs autres publications de Lemaître [118], notamment l'ouvrage qui fera le plus connaître Lemaître en Europe et à l'étranger : L'hypothèse de l'atome primitif : Essai de cosmogonie, publié à Neuchâtel et à Bruxelles en 1946, traduit en anglais sous le titre The primeval atom : An essay on cosmogony en 1950.
En fait, cet ouvrage n'est pas un texte original de Lemaître, mais une collection de cinq articles déjà existants. Le chapitre 1, intitulé <<La grandeur de l'espace>>, est le texte d'une conférence faite le 31 janvier 1929 à la Société scientifique de Bruxelles et publiée dans la Revue des Questions Scientifiques en mars 1929. Le chapitre 2, intitulé <<Expansion>>, reprend l'article <<L'expansion de l'espace>> paru dans la Revue des Questions Scientifiques en novembre 1931 (cf. infra page xxx). Le chapitre 3, intitulé <<Évolution>>, est le texte d'une lecture publique devant l'Académie royale de Belgique le 15 décembre 1934, publiée sous le titre <<L'Univers en Expansion>> dans le Bulletin de l'Académie en décembre 1934. Le chapitre 4, intitulé <<Hypothèses cosmogoniques>>, reprend la conférence du même nom faite à la Société royale belge des Ingénieurs et des Industriels, à Bruxelles le 10 janvier 1945, et publiée dans Ciel et Terre en mars -avril 1945. Enfin, le chapitre 5 reprend le texte de 1945 qui donne son titre à l'ouvrage et que nous publions ici (cf. infra page xxx). Lemaître a écrit une brève introduction supplémentaire, ainsi qu'une vingtaine de pages d'éclaircissements mathématiques figurant en appendice. Le tout est préfacé par Ferdinand Gonseth [119].
Le livre paraît en quelque sorte à contretemps, car la théorie de l'atome primitif n'est plus à la mode. Lemaître lui-même ne s'intéresse plus que de loin à la cosmologie, même s'il donne encore régulièrement des conférences un peu partout en Europe. La grande passion scientifique de Lemaître est désormais le calcul numérique sur machine, domaine où il sera aussi grand précurseur. Depuis 1948 triomphe la théorie cosmologique alternative de l'<<état stationnaire>>, dont les promoteurs principaux sont l'américain Thomas Gold et les britanniques Hermann Bondi et Fred Hoyle [120]. Leur idée est que l'univers a toujours été et sera toujours comme il est maintenant, identique à lui-même au cours du temps (d'où le nom de l'état stationnaire). Mais comme la matière cosmique se disperse sous l'effet de la fuite des galaxies, les auteurs de l'état stationnaire proposent, pour compenser la dilution et assurer une densité moyenne constante, que de la matière soit créée spontanément, de façon continue - d'où le nom également donné à cette théorie : la <<création continue>>.
Fred Hoyle, à la forte personnalité, n'est guère tendre avec ses adversaires scientifiques. Lors d'une réunion à Pasadena en 1960, Hoyle se moque de Lemaître en l'accueillant par ces mots: <<This is the Big Bang man>>. Hoyle apportera pourtant doublement de l'eau au moulin de la théorie du Big Bang : d'abord en lui trouvant son nom (qui pour lui était signe de dérision), et plus sérieusement en contribuant à résoudre la question de l'abondance des éléments chimiques dans l'Univers. L'expression Big Bang, débarrassée de son sens péjoratif, allait passer à la postérité grâce à un américain d'origine russe, ancien étudiant de Friedmann mais que Lemaître ne voulut pas rencontrer: Georges Gamow.
Gamow reprend les données de physique nucléaire développées pour des projets militaires et propose une théorie de l'origine des éléments. Il émet l'hypothèse que tous les éléments ont été produits durant les premières phases, très chaudes, de l'univers en expansion. Grâce aux travaux de Fred Hoyle et de ses collaborateurs, cette vue sera ultérieurement corrigée : seuls les isotopes les plus légers - hydrogène, hélium, lithium - ont pu se former dans l'univers chaud du début selon le processus envisagé par Gamow; les éléments plus lourds, comme le carbone, l'azote, l'oxygène, etc., proviennent des étoiles explosives, d'une époque beaucoup plus récente.
Quoi qu'il en soit, Gamow a enrichi considérablement l'hypothèse de Lemaître en y ajoutant la notion de température. Lemaître imaginait que l'univers du début devait être plus dense, Gamow a précisé qu'il devait être également plus chaud. Ce nouveau paramètre de température est le vrai trait d'union entre la cosmologie et la physique des particules à haute énergie, disciplines qui marchent aujourd'hui de pair et dont Lemaître avait entrevu le mariage dès 1931.
C'est aussi la raison pour laquelle Lemaître s'est trompé en cherchant dans les rayons cosmiques le vestige de l'univers primitif : il fallait chercher un rayonnement thermique. C'est précisément ce que fit Gamow, qui prédisit un vestige sous forme d'un rayonnement de corps noir à la température de 5 Kelvin (dans la gamme des micro-ondes). Ce rayonnement a été découvert en 1965 par Arno Penzias et Robert Wilson, à la température de 3 Kelvin, et interprété théoriquement par Robert Dicke et James Peebles [121]. C'est Odon Godart qui a appris à Mgr Lemaître, quelques jours avant sa mort, la découverte du rayonnement fossile - ce que Lemaître avait élégamment appelé <<l'éclat disparu de la formation des mondes>>. Lemaître avait été transporté à l'hôpital deux semaines auparavant, atteint d'une leucémie. Lemaître dit simplement <<Je suis content maintenant, au moins, on en a la preuve>>.
Le fait est que l'hypothèse de l'atome primitif devenait enfin, sous le nom plus médiatique de Big Bang, une théorie physique. Quelques années supplémentaires seront nécessaires pour qu'elle reçoive ses titres de noblesse: le prix Nobel de Physique sera remis à Penzias et Wilson le 8 décembre 1978.
Nous terminerons cette rapide exégèse de l'oeuvre cosmologique de Friedmann et Lemaître en examinant l'une de leurs contributions qui, curieusement, n'a pratiquement été relevée par aucun de leurs commentateurs, mais qui constitue pourtant l'un des signes les plus remarquables de leur originalité : la topologie de l'espace. Friedmann et Lemaître se sont en effet penchés non seulement sur la dynamique cosmique, mais aussi sur la structure globale de l'univers, c'est-à-dire sa topologie. De plus, ils ont tous deux rapidement pris conscience de l'incomplétude de la théorie de la relativité générale sur ce problème.
L'une des plus anciennes questions cosmologiques est celle de l'extension de l'espace. Est-il fini ou infini? L'espace physique newtonien, mathématiquement identifié à l'espace euclidien infini, n'était pas sans poser quelques paradoxes, tels celui dit d'Olbers [122], et autres problèmes de conditions aux limites; si l'on se réfère par exemple au principe de Mach, qui a tant guidé Einstein dans l'élaboration de la relativité générale, et en vertu duquel l'inertie locale est la résultante des contributions des masses à l'infini, un problème évident de divergence se pose dès lors que l'espace infini, s'il est homogène, a une masse infinie.
Lorsqu'Einstein introduisit dans son modèle cosmologique de 1917 un espace tridimensionnel de courbure positive (appelé aussi hypersphère), l'une de ses principales motivations était de fournir un modèle d'espace fini, bien que sans frontières. Cette solution résolvait de façon si ingénieuse tous les paradoxes liés à l'espace newtonien que les cosmologistes s'accrochèrent rapidement à cette idée nouvelle, aux dépens des autres possibilités.
Einstein pensait aussi que l'hypershère fournissait non seulement la métrique de l'espace - c'est-à-dire ses propriétés géométriques locales - mais aussi sa structure globale, sa topologie; par exemple, le fait que le volume de l'espace soit fini. Or, la question de la forme globale de l'espace, ou plus généralement de son caractère fini ou infini, n'est pas seulement affaire de métrique; c'est avant tout affaire de topologie et à ce titre, exige une approche supplémentaire par rapport à celle de la géométrie différentielle riemannienne - support mathématique de la relativité générale.
Les équations d'Einstein étant des équations aux dérivées partielles, elles ne décrivent que les propriétés géométriques locales de l'espace-temps. Ces dernières sont contenues dans le tenseur métrique, qui permet notamment de calculer les composantes de courbure en chaque point de l'espace-temps. Mais les équations d'Einstein ne fixent pas la structure globale de l'espace-temps: pour une métrique donnée, solution des équations, correspondent plusieurs - et même en général une infinité - de modèles d'univers topologiquement distincts.
Mathématiquement, un espace est dit posséder une topologie simplement connexe si en chacun de ses points, toute courbe fermée peut être continûment contractée en un point; c'est le cas, par exemple, du plan euclidien infini ou de la surface d'une sphère. Dans le cas contraire, la topologie est dite multiplement connexe. Toute surface qui possède par exemple un trou (comme un tore ou une sphère munie d'une poignée) est multiplement connexe.
Pour une métrique donnée, la topologie la plus simple est celle de l'espace simplement connexe ayant localement cette métrique. Mais la pertinence physique ne se mesure pas nécessairement à l'aune de la simplicité mathématique. Les variétés riemanniennes utilisées en relativité générale sont moins <<simples>> que l'espace euclidien. Dès lors, qu'est-ce qui peut guider le choix du physicien en matière de topologie?
La topologie ne faisait apparemment pas partie des préoccupations d'Einstein, puisque son article de 1917 ne mentionne aucune alternative topologique à son modèle d'espace sphérique. Aussitôt, certains de ses collègues, plus au fait des développements récents de la topologie, lui firent remarquer le caractère arbitraire de son choix. De Sitter, par exemple, nota que la solution cosmologique d'Einstein admettait une forme différente de l'espace sphérique : celle de l'espace projectif tridimensionnel (appelé aussi <<espace elliptique>>), construit à partir de la sphère en identifiant les points diamétralement opposés. L'espace projectif a la même métrique que l'espace sphérique, mais une topologie différente - notamment son volume est moitié moindre.
Hermann Weyl lui écrivit également sur la question du choix entre les topologies sphérique ou elliptique. Einstein lui répondit dans une lettre [123] datée de juin 1918 : <<J'ai pourtant un sentiment obscur qui me fait préférer le [modèle] sphérique. Je pressens que les variétés dans lesquelles toute courbe fermée peut être contractée continûment en un point sont les plus simples. D'autres personnes doivent également avoir ce sentiment, car autrement, en astronomie, on aurait sans doute pris en considération le cas que notre espace puisse aussi être euclidien et fini. L'espace euclidien à deux dimensions aurait alors les propriétés de connexion d'une surface annulaire. C'est un plan euclidien dans lequel tout phénomène est doublement périodique, où des points qui se trouvent sur la même grille périodique sont identiques. Dans l'espace euclidien fini existeraient trois genres de courbes fermées non continûment réductibles en un point. De façon analogue, l'espace elliptique possède, contrairement au sphérique, une classe de courbes non continûment réductibles en un point; c'est pourquoi il me plaît moins que le sphérique. Peut-on prouver que l'espace elliptique est la seule variante de l'espace sphérique ? Il me semble>>.
Einstein répète cet argument dans une carte postale [124] du 16 avril 1919 adressée cette fois à Félix Klein : <<Je voudrais vous soumettre un argument par lequel la possibilité sphérique semble devoir être préférée à la possibilité elliptique. Dans l'espace sphérique, toute courbe fermée peut se contracter continûment en un point, mais pas dans l'espace elliptique; autrement dit seul l'espace sphérique, et non pas l'elliptique, est simplement connexe. [...] Il y a sans doute pour l'élément de métrique euclidien des espaces finis d'étendue arbitraire, que l'on peut obtenir à partir des espaces infinis en postulant une triple périodicité [125], si l'on suppose l'identité entre certains points. Mais ces possibilités-là, qui n'entrent pas en considération pour la relativité générale, souffrent de la propriété que les espaces correspondants sont multiplement connexes>>. Ainsi, sans autre argumentation physique, Einstein avait un préjugé "esthétique" en faveur du caractère simplement connexe de l'espace.
Dans sa réponse à Weyl, Einstein se trompait notamment sur le dernier point : à trois dimensions, en plus de l'espace elliptique existe une infinité de variantes topologiques de l'espace sphérique, toutes fermées, comprenant notamment les espaces dits <<lenticulaires>> [126] (tandis que pour les surfaces bidimensionnelles de courbure positive, il n'y a effectivement que deux types topologiques distincts, la sphère et le plan elliptique). Mais cela, personne ne le savait encore. La classification topologique des espaces tridimensionnels commençait à peine à être comprise. L'étude des différentes formes d'espace euclidien à trois dimensions avait commencé avec des travaux de cirstallographie. Le russe Feodoroff avait classé les 18 groupes de symétrie pour les structures cristallines dans R3 en 1885, et en 1911, Bierbach avait élaboré une théorie des groupes cristallographiques [127]. Ce n'est toutefois qu'en 1934 que Nowacki [128] démontrera comment les résultats de Bierbach permettent de classifier les formes d'espace euclidien. Le cas des espaces sphériques avait été posé notamment par Félix Klein en 1890 et par Killing en 1891, sous le nom de problème de Clifford-Klein [129]. Ce problème ne sera résolu de façon complète qu'en 1960 par Wolf [130]. Quant au problème des espaces homogènes hyperboliques, la classification ne commencera à être abordée sérieusement que dans les années 1970 par W. Thurston [131], et fait aujourd'hui encore l'objet de recherches intensives.
La découverte des solutions non statiques par Friedmann en 1922, et par Lemaître en 1927, enrichit considérablement le champ de la modélisation cosmologique. Les modèles d'univers homogènes et isotropes admettent des espaces de type sphérique, euclidien ou hyperbolique selon que leur courbure spatiale (constante) est positive, nulle ou négative. Dans son ouvrage de vulgarisation, Friedmann mentionne déjà le problème topologique et il insiste sur le fait que la métrique, donc la relativité générale, ne suffit pas à elle seule à définir la structure globale de l'espace. Pour en décider il faut des hypothèses supplémentaires. Il indique notamment l'exemple du cylindre; cette surface à deux dimensions est une variante topologique du plan euclidien obtenue en identifiant les bords opposés d'une bande plane de longueur infinie. Le cylindre est bien une surface localement euclidienne (sa courbure est partout nulle), mais elle est finie dans une direction et infinie dans l'autre.
Les remarques les plus profondes de Friedmann sur la question topologique se trouvent dans l'article de 1924. Il est le premier à définir clairement les limitations fondamentales de la théorie cosmologique fondées sur la relativité générale. <<En l'absence d'hypothèses additionnelles, les équations d'univers d'Einstein ne permettent pas de trancher la question de la finitude de notre univers>>, écrit-il. Il s'attache à définir comment l'espace peut devenir fini si l'on identifie des points entre eux (ce qui, en langage topologique, rend l'espace multiplement connexe). Il entrevoit aussi comment cette possibilité permet l'existence de "fantômes", en ce sens qu'en un même point coexistent un objet et ses propres images. <<Un espace à courbure positive est toujours fini>>, ajoute-t-il, mais les connaissances mathématiques ne permettent pas de <<résoudre la question de la finitude pour un espace à courbure négative>>. On le voit, Friedmann n'avait aucun préjugé en faveur de la topologie simplement connexe, ni n'avouait sa préférence pour une topologie particulière.
De son côté, Lemaître partage pleinement le penchant commun en faveur de la finitude de l'espace. Dans une conférence devant l'Institut Catholique de Paris [132], dans laquelle il parle du développement de la géométrie au XIXe siècle, il décrit la géométrie riemannienne comme celle qui a <<dissipé le cauchemar de l'espace infini>>. Tous les modèles cosmologiques pour lesquels il a opté à partir de 1927 font l'hypothèse d'un espace de courbure positive, nécessairement fini. Ceci ne l'empêche nullement de reconnaître d'autres possibilités. Il est, semble-t-il, le premier cosmologiste à remarquer, en 1958, que les métriques de courbure négative admettent des topologies de volume fini : <<Il est vrai qu'un espace localement hyperbolique n'est pas nécessairement ouvert. Il est possible de construire de tels espaces ayant un volume fini. Cela est même vrai pour l'espace euclidien>> [133]. Par ailleurs, Lemaître discute longuement la possibilité de l'espace elliptique, notamment dans son texte de 1931 ; contrairement à Einstein, il lui donne sa préférence, mais son argumentation semble tout autant reposer sur un <<sentiment esthétique>>.
Ces idées extrêmement fécondes de la topologie resteront largement ignorées du courant général de la cosmologie, hormis quelques exceptions [134]. Le modèle d'Einstein-de Sitter de 1932, qui stipule un espace euclidien, fait implicitement l'hypothèse du caractère infini de l'espace. L'oubli quasi-total de l'aspect topologique remonte à cette période. Les articles et les manuels - spécialisés ou non - traitant de cosmologie supposent implicitement que la structure spatiale de l'univers est soit l'hypersphère finie, soit l'espace euclidien infini, soit l'espace hyperbolique infini, sans mentionner les alternatives topologiques. Peu à peu, cette simplification arbitraire instaure une confusion sur le qualificatif <<ouvert>> ou <<fermé>>, utilisé pour caractériser les modèles de Friedmann-Lemaître. On croit qu'il s'applique non seulement au comportement temporel des modèles (ouverts s'ils sont en expansion perpétuelle, fermés s'ils sont en expansion-contraction), mais aussi à son caractère spatial. Dans l'hypothèse d'une topologie simplement connexe et d'une constante cosmologique nulle, il y a en effet stricte coïncidence entre modèles en expansion perpétuelle et modèles spatialement infinis d'une part, entre modèles en expansion-contraction et modèles spatialement finis d'autre part. Mais selon l'avertissement de Friedmann, pour savoir si l'espace est fini ou infini, il ne suffit pas de déterminer le signe de la courbure spatiale, autrement dit de comparer la densité de matière à la <<densité critique>>; il faut des <<hypothèses supplémentaires>> - précisément, celles de la topologie.
Aujourd'hui, les investigations sur la topologie cosmique ont peu progressé. Le préjugé en faveur des espaces simplement connexes plutôt que multiplement connexes rappelle le préjugé des années 1920-30 en faveur des espaces statiques plutôt que dynamiques. Le principe d'économie, en vertu duquel le nombre minimal d'hypothèses est préférable dans la construction d'un modèle, permet à première vue de sélectionner la topologie simplement connexe. Pourtant, de nouvelles approches de l'espace-temps, comme celle de la cosmologie quantique, suggèrent la nécessité d'un volume spatial fini. Par ailleurs, les données astronomiques présentes indiquent que la densité de matière dans l'univers observable est inférieure à la valeur critique, donc une solution de Friedmann-Lemaître à espace hyperbolique. Or, un espace hyperbolique n'a un volume fini que si sa topologie est multiplement connexe...
Parmi les observations astronomiques directes susceptibles de mettre en évidence la topologie de l'espace, figure la recherche de ces <<images fantômes>> dont parlait Friedmann dans son article de 1924, c'est-à-dire des images multiples d'un seul et unique objet céleste. Les images fantômes peuvent apparaître dans un espace topologiquement fini et dont le volume est plus petit que celui de l'espace observable, parce que la lumière émise par une source lointaine peut nous atteindre selon plusieurs trajets spatio-temporels. L'école russe a été la plus active dans le domaine; un programme observationnel, commencé dans les années 1970 au télescope de six mètres de Zelentchouk (Caucase) sous la direction de Viktoryn Fyodorovich Schvartsman, a permis de fixer des contraintes sur la taille minimale d'un espace multiplement connexe. De nouveaux tests observationnels, dans l'hypothèse d'un <<univers cristallographique>>, ont récemment été proposés [135].
Le domaine de la topologie cosmique émerge peu à peu de l'ombre. S'il sort un jour en pleine lumière, il faut espérer qu'Alexandre Friedmann et Georges Lemaître y feront figure d'éclaireurs.
*
[1] Thomas S. Kuhn, La structure des révolutions scientifiques, trad. fr. L. Meyer, Flammarion, 1983.Retour texte
[2] Nicolas Copernic, De Revolutionibus Orbium Coelestis, trad. fr. Sur les révolutions des orbes célestes, Blanchard, Paris, 1987.Retour texte
[3] Tycho Brahé, Astronomiae instauratae Progymnasmata, Prague 1603. Dans Tychonis Brahe Danis Opera Omnia, ed. J.L.E. Dreyer, 15 vols., Copenhagen Libraria Gyldendaliana, 1913-1929. Aucune traduction en français de cet ouvrage fondamental n'est disponible. Retour texte
[4] Voir par exemple Giordano Bruno, De l'infini, de l'univers et des mondes, Oeuvres complètes, vol. IV, trad. fr. J.-P. Cavaillé, Les Belles Lettres, 1995.Retour texte
[5] Johannes Kepler, Astronomia Nova, trad. fr. Astronomie nouvelle, Blanchard, Paris, 1984.Retour texte
[6] Galilée, Le Messager Céleste, trad. fr. Le Seuil/Sources du Savoir, Paris, 199xRetour texte
[7] En ce qui concerne les rapports entre les révolutions astronomiques et la littérature, voir H. Tuzet, Le Cosmos et l'Imagination, José Corti, Paris, 1965, et Jean-Pierre Luminet, Les poètes et l'univers, Le Cherche-Midi éditeur, Paris, 1996.Retour texte
[8] Merleau-Ponty, Cosmologies du XXe siècle, Paris, Gallimard, 1965, page 8.Retour texte
[9] Voir par exemple Jean-François Gautier, L'Univers existe-t-il ?, Actes Sud, 1994.Retour texte
[10] Pour ce qui est des anthologies, toutes en langue anglaise, Milton Munitz, Theories of the Universe: From Babylonian Myth to Modern Science (cf. Bibliographie générale en fin de volume, ainsi que pour les références qui suivent) propose, depuis le Timée de Platon (vers 355 av. J.-C.) jusqu'à Fred Hoyle (1950), un ensemble de textes marquant des jalons importants dans l'évolution de la pensée cosmologique occidentale. Cette anthologie de la littérature cosmologique comporte un article de Lemaître, mais aucun de Friedmann. La période relativiste entre 1917 et 1982 est traitée dans les anthologies de Jeremy Bernstein et Gerald Feinberg, Cosmological Constants, et de Kenneth Lang et Owen Gingerich, A Source Book.. Pour ce qui est des analyses, nous citerons le monumental travail de Pierre Duhem, Le Système du Monde, en ce qui concerne la période pré-copernicienne, Alexandre Koyré, Du monde clos à l'univers infini et Etudes Newtoniennes pour la période ultérieure et, pour les cosmologies du XXe siècle, Jacques Merleau-Ponty, Cosmologies du XXe siècle, et George Ellis, <<Cosmology from 1917 to 1960>>.Retour texte
[11] Transcrite littéralement du russe, l'orthographe correcte serait Fridman, voir par exemple l'article de V. Fock, qui fut son élève : <<The researches of A.A. Fridman on the Einstein theory of gravitation>>. Sov. Phys. Usp. 6(4) (1964) pp. 473-474. Dans l'article de 1922 paru dans Zeits. f. Physik, l'orthographe est Friedman. C'est Einstein qui, semble-t-il, a introduit la variante <<Friedmann>> dans sa <<remarque sur le travail de A. Friedmann>> parue la même année dans Zeits. f. Physik. Cette orthographe a prévalu, à tel point que le second article du physicien russe paru dans Zeits. f. Physik en 1924 est signé Friedmann! Nous adopterons donc ici l'orthographe d'usage (usage tout relatif, dans la mesure où Alexandre Friedmann ne figure pas dans le Dictionnaire Robert des Noms Propres).Retour texte
[12] Biographical Encyclopedia of Scientists, second edition, Institute of Physics Publishing, Bristol and Philadelphia, 1994.Retour texte
[13] Inventeurs et Scientifiques, Larousse, 1994.Retour texte
[14] Dictionary of Scientific Biography, Ed. C.C. Gillespie, 16 vols. New York: Scribner, 1970-80.Retour texte
[15] H.P. Robertson, <<Relativistic Cosmology>>, Rev. Mod. Phys. 5, 62, 1933.Retour texte
[16] Voir la remarquable analyse de Jean-François Robredo, La contribution de Georges Lemaître à la cosmologie moderne, cf. bibliographie générale.Retour texte
[17] Voir la Bibliographie générale.Retour texte
[18] Lire par exemple P.J.E. Peebles, <<Impact of Lemaitre's Ideas on Modern Cosmogy>>, in Berger 1984 (bibliographie générale); Joseph Silk, The big bang, édition revue et réactualisée, New York, Freeman, 1989. Il est vrai que Silk séjourne fréquemment en Europe, qu'il en connaît la culture et les traditions. Quant à Peebles, il a reçu le premier Prix attribué par la Fondation Lemaître en 1994.Retour texte
[19] George Smoot et Keay Davidson, Wrinkles in Time, W. Morrow and Co, New York, 1994; trad. fr. Les rides du temps, Flammarion, Paris, 1994.Retour texte
[20] George Ellis, dans <<Cosmology from 1917 to 1960>>, distingue également des périodes, mais avec un découpage différent.Retour texte
[21] Rappelons que le terme de <<big bang>> est devenu célèbre du jour au lendemain, à la suite d'une émission de la radio britannique au cours de laquelle Fred Hoyle, l'adversaire le plus acharné de la théorie de Lemaître et promoteur de la théorie alternative de l'état stationnaire, l'avait utilisé par dérision.Retour texte
[22] Nous remercions André Berger, directeur de l'Institut d'Astronomie et de Géophysique G. Lemaître à Louvain, qui a accordé les autorisations de publication, et Jacqueline Moens, conservatrice des Archives, qui a faciltié la consultation des Archives.Retour texte
[23] Pour un développement plus complet, voir par exemple Jean-Pierre Luminet, Les trous noirs ; Première partie : Gravitation et lumière, Paris, Le Seuil / Points Sciences, 1992.Retour texte
[24] Aristote, Physique, trad. fr., Garnier-Flammarion, 1995.Retour texte
[25] Isaac Newton, De Philosophiae Naturalis Principia Mathematica, 1687 ; trad. fr. : Principes Mathématiques de la Philosohie Naturelle, Bourgois, Paris, 1985Retour texte
[26] James Clerk Maxwell, Treatise on Electricity and Magnetism ,Oxford, Oxford University Press, 1873. ; trad. fr. : Traité d'Electricité et de Magnétisme, Jacques Gabay, Paris, 1989.Retour texte
[27] Pour les références précises concernant la période postérieure à 1900, nous renvoyons le lecteur à A. Einstein, Oeuvres choisies, volume 2: Relativités I, coll. Sources du Savoir, Le Seuil/CNRS, Paris, 1993.Retour texte
[28] Trad. fr. dans Oeuvres choisies, volume 2: Relativités I, p.134.Retour texte
[29] Trad. fr. dans Oeuvres choisies, volume 2: Relativités I, p.169.Retour texte
[30] A. Einstein, <<Die Feldgleichungen der Gravitation>>, Preussische Akademie der Wissenschaften, Sitzungsberichte, 1915, p. 844-847.Retour texte
[31] En fait, le théorème d'Emmy Noether sera démontré en 1918 dans un article publié sous son propre nom. Ce théorème est devenu en physique théorique un outil vital, dont la portée est beaucoup plus générale que le seul cadre initial d'une théorie de la gravitation. En 1917, Weyl découvrit un cas particulier du théorème de Noether en dérivant des identités qui avaient été découvertes indépendamment par Ricci en 1889 et par Bianchi en 1902.Retour texte
[32] A. Einstein, <<Die Grundlage der allgemeinen Relativitätstheorie>>, Annalen der Physik, vol. XLIX, 1916, p. 769-822. Trad. franç. <<Les fondements de la théorie de la relativité générale>>, in A. Einstein, Oeuvres choisies, volume 2: Relativités I, p. 179 sq.Retour texte
[33] Preussische Akademie der Wissenschaften, Sitzungsberichte, 1917, p. 142-152.Retour texte
[34] <<Considérations cosmologiques sur la théorie de la relativité générale>>, dans Einstein, Oeuvres choisies, vol. 3, Relativités II, p. 88-98.Retour texte
[35] Le travail d'Ernst Mach sur la gravité et l'origine de l'inertie est Die Mechanik in ihrer Entwicklung, historisch-kritisch dargestellt, Leipzig, Brockhaus, 1883.Retour texte
[36] <<Considérations cosmologiques...>>, p. 97.Retour texte
[37] En 1967, le physicien soviétique Zel'dovich a montré qu'à la lumière de la théorie quantique des champs, l'incorporation de l dans le tenseur impulsion-énergie pouvait être non pas seulement formelle, mais physiquement justifiée; en effet, le vide quantique apporte une contribution au tenseur impulsion-énergie de la forme . Voir Ya. B. Zel'dovich, <<Cosmological constant and elementary particles>>, Soviet Physics JETP Letters, 6, 316-317, 1967.Retour texte
[38] <<Considérations cosmologiques...>>, p. 98Retour texte
[39] W. de Sitter, <<On Einstein's Theory of Gravitation and its Astronomical Consequences>>, Monthly Notices of the Royal Astronomical Society, vol. 78, 1917, p. 3-28. Dans son article de revue de 1933, H. P. Robertson attribue l'idée de l'univers de De Sitter à l'un de ses collègues hollandais, Paul Ehrenfest.Retour texte
[40] V.M. Slipher, <<Spectrographic Observations of Nebulae>>, Pop. Ast. 23, 21-24, 1915. L'auteur fait état de quinze vitesses radiales mesurées, dont onze sont positives.Retour texte
[41] Sur les discussions entre Einstein et de Sitter qui ont suivi, nous renvoyons le lecteur à Relativités II, p. 98-102, et surtout à Pierre Kerszberg, <<The Einstein-de Sitter Controversy of 1916-1917 and the Rise of Relativistic Cosmology>>, in Howard et Stachel, bibliographie générale.Retour texte
[42] Le lecteur intéressé trouvera une description exhaustive de sa vie et de son oeuvre dans E. Tropp, V. Frankel et A. Chernin, voir Bibliographie.Retour texte
[43] Selon son ancien élève George Gamow, Friedmann aurait succombé à une pneumonie contractée lors de son vol en ballon. Cf. G. Gamow, My World Line : An Informal Autobiography, Viking Press, New York, 1970.Retour texte
[44] V.K. Frederiks, Uspekhi Fizicheskikh Nauk (Advances in Physical Sciences) vol.2 p.162 (1922).Retour texte
[45] V.K. Frederiks et A. A. Friedman, Osnovy teorii otnositel'nosti (Principes de la Théorie de la Relativité), I: Tenzorial'noe ischislenie (Calcul Tensoriel), Akademia,1924.Retour texte
[46] Cité par Jean-Marc Lévy-Leblond, <<L'arbre et la forêt : le mythe d'Einstein>>, in L'esprit de sel, Le Seuil / Points Sciences, Paris, 1984, p. 164.Retour texte
[47] Nous en avons supprimé certaines dans la traduction ci-après.Retour texte
[48] Trad. franç. : Fondements de la Géométrie, par P. Rossier, Paris, Dunod, 1971.Retour texte
[49] Nicolas Bourbaki, auteur polycéphale formé à partir de 1933 par des mathématiciens de l'Ecole normale supérieure, reprendra les mathématiques modernes dans leurs fondements pour l'édifier sur des bases axiomatiques rigoureuses dans l'esprit de Hilbert.Retour texte
[50] Ernest Nagel, James R. Newman, Kurt Gödel, Jean-Yves Girard, Le théorème de Gödel, Paris, Le Seuil, 1989 (collection Sources du Savoir).Retour texte
[51] B. Riemann, Gesammelte mathematische Werke, 2e éd., Leipzig, Teubner, 1892, p. 276.Retour texte
[52] C. F. Gauss, vol. VIII p.201 in Werke, 12 volumes, Göttingen, 1870-1927. Retour texte
[53] G. Boole, The mathematical analysis of logic, Cambridge, 1847.Retour texte
[54] Ce point de vue, encore dominant, n'est pas le seul ; on peut aussi considérer la relativité générale comme une théorie des champs non linéaire, voir par exemple Jean-Marc Lévy-Leblond, Aux contraires, Gallimard, 1996, note 2 p. 110 et références indiquées. Retour texte
[55] Un ouvrage excellent traitant de l'analyse tensorielle dans un contexte très large est J.A.Schouten, Ricci-Calculus (Springer, 2nd ed. 1954), en particulier chap. 3 <<Linear connexions>>.Retour texte
[56] Publiées par l'Académie royale de Belgique.Retour texte
[57] Cf. A. Einstein, Relativités II , partie III.Retour texte
[58] T. Kaluza, <<Zum Unitätsproblem der Physik>>, Sitzungsberichte Preussische Akademie der Wissenschaften, 1921, p. 966-972, et O. Klein, Zeitschrift für Physik, vol. XXXVII, 1926, p. 895-906.Retour texte
[59] L'analogie est de Andrey Grib, <<Concepts of modern physics for economists>>,Retour texte
St.Petersburg University of Economics and Finances, St.Petersbourg, Russie.
[60] Pour une approche vulgarisée, voir par exemple Paul Davies, Superforce, Payot, 1987.Retour texte
[61] A. A. Friedmann et J. A. Schouten, <<Über die Geometrie der halbsymmetrischen Übertragungen>>, Math. Zeitschrift, 21, 3-4, 1924.Retour texte
[62] Sur le point de vue moderne concernant la singularité cosmique - par exemple le fait de savoir si elle est une conséquence inéluctable de la relativité générale, si elle a eu lieu en un seul point ou plusieurs, etc., le lecteur pourra consulter S.W. Hawking et G.F.R. Ellis, The Large Scale Structure of Spacetime, Cambridge University Press, 1973, et, à un niveau moins technique, S. Hawking et R. Penrose, La Nature de l'espace et du temps, Gallimard, 1997.Retour texte
[63] Andrey Grib, communication privée.Retour texte
[64] A. Eddington, La nature du monde physique (trad. fr. G. Gros), Paris, Payot, 1929, p.99. Il s'agit de conférences données de janvier à mars 1927 à l'université d'Edimbourg.Retour texte
[65] Voir par exemple Jacques Demaret, Univers, Le Mail, 1991, [[section]] 7.9.Retour texte
[66] Certaines conjectures sur des solutions possibles peuvent être trouvées dans S.W. Hawking, Une brève histoire du temps, Paris, Champs Flammarion, 1991; Andrei Linde, Particle Physics and Inflationary Cosmology, Harwood, 1990 ; Jacques Demaret et Dominique Lambert, Le Principe Anthropique, Paris, Armand Colin, 1994.Retour texte
[67] Cet article a été traduit en russe sous le titre <<O krivizne prostranstva >>, Zhurnal Russkago fiziko-khimicheskago obshchestva, vol. 56 ndeg.1 (1924) p. 40-58, et dans Uspekhi Fizicheskikh Nauk, vol. 80 ndeg.3 (1963) pp. 439-446. Traduction anglaise : << On the curvature of space >>, par B. Doyle, in K.R. Lang et 0. Gingerich (éd.), A Source Book in Astronomy and Astrophysics, 1900-1975, Cambridge, Mass., Harvard University Press, 1979, p. 838.Retour texte
[68] Equations (4) et (5), cf. infra, p. ...Retour texte
[69] A. Einstein, Zeitschrift für Physik 11, 326 (1922). Trad. franç. <<Remarque sur le travail de A. Friedmann <<Sur la courbure de l'espace>> >> in Einstein, Oeuvres choisies, vol. 3, Relativités II, p. 103.Retour texte
[70] Son objection repose sur l'équation au lieu de , où [[rho]] est la densité, R le rayon d'univers et x4 la variable temporelle.Retour texte
[71] Pour la suite de cette section, nous suivons de près l'article de V. Frenkel et A.A.Grib, Proc. of the 2nd Alexander Friedmann International seminar on Gravitation and Cosmology, St Petersburg, Friedmann Laboratory Publishing 1994, p. 1.Retour texte
[72] Equivalente à l'équation de la note ci-dessus.Retour texte
[73] Lettre du 28 octobre 1920. Voir A. Einstein, M. Born, Correspondance 1916-1955, Paris, Le Seuil, 1972.Retour texte
[74] A. Einstein, Zeitschrift für Physik 21, 228, 1923. Trad. franç. <<Note sur le travail de A. Friedmann <<Sur la courbure de l'espace>> >> in Einstein, Oeuvres choisies, vol. 3, Relativités II, p. 104-105.Retour texte
[75] J. Stachel, <<Eddington and Einstein>>, in E. Ulmann-Margarit (éd.), The Prism of Science, Dordrecht et Boston, D. Reidel, 1986.Retour texte
[76] Voir notamment l'analyse de J. Eisenstaedt dans Einstein, Oeuvres choisies, vol. 3, Relativités II, pp. 83-129.Retour texte
[77] Emmanuel von der Pahlen (1882-1952), astronome allemand travaillant à l'Observatoire de Postdam, surtout connu pour ses travaux sur la statistique stellaire. Docteur en Philosophie de l'université de Göttingen, il avait vécu à Saint-Petersbourg et avait été l'assistant de Friedmann à Kiev. Il était parti en Allemagne après la révolution de 1917. En 1924, il publia un ouvrage intitulé L'infini de l'espace et la théorie de la Relativité.Retour texte
[78] voir K. Hentschel, <<Erwin Finlay Freundlich and Testing Einstein's Theory of Relativity>>, Archive for History of Exact Sciences, 47, 143-201, 1994. Sur l'ensemble de sa vie et son oeuvre, voir Dictionary of Scientific Biography.Retour texte
[79] L'article a été traduit en russe dans Uspekhi Fizicheskikh Nauk vol. 93 ndeg.2 (1967) pp. 280-287, et en anglais dans Bernstein et Feinberg, op. cit. Retour texte
[80] H.P. Robertson et T.W. Noonan, Relativity and Cosmology, Philadelphie, W.B.Saunders, 1968.Retour texte
[81] G. Lemaître, La théorie de la relativité et l'expérience, in Revue des Questions Scientifiques, 4e série, t. IX, 1926, pp. 346-374.Retour texte
[82] cf. Bibliographie en fin de volume.Retour texte
[83] Pour ce résumé biographique, nous suivons de près l'excellent résumé de Odon Godart, <<Monseigneur Lemaître, sa vie, son oeuvre>>, Revue des Questions Scientifiques, vol. 155, 1984, p. 155-182.Retour texte
[84] Traduit en français sous le titre Espace, Temps et Gravitation, Paris, Hermann, 1921.Retour texte
[85] Arthur S. Eddington, The Mathematical Theory of Relativity, Cambridge, Cambridge University Press, 1922.Retour texte
[86] Pour la question de l'influence d'Eddington sur Lemaître, cf. D. Lambert, Un atome d'univers, en préparation.Retour texte
[87] Georgy Abramovich Grinberg, étudiant de Friedmann, avait soutenu en 1924 une thèse sur le même sujet : G.A. Grinberg. J. Russ. Phys. Chem. Soc., vol. 56, p.368, 1925, restée ignoré car en langue russe.Retour texte
[88] H. Weyl, Zeit. Phys. 24, 230 (1923)Retour texte
[89] G. Lemaître, <<Note on De Sitter's universe>>, The Physical Review, t. XXV, 1925, p. 903. <<Note on De Sitter's universe>>, Journal of Mathematics and Physics, t. IV, 1925, p. 189-192.Retour texte
[90] Voir Encadré 1. Cette forme sera plus tard utilisée pour décrire l'hypothétique phase inflationnaire des modèles de big bang. Voir par exemple Andrei Linde, Particle physics and inflationary cosmology, Harwood, 1990.Retour texte
[91] Sur la vie et l'oeuvre de Hubble, voir Bibliographie générale. Après la mort de l'astronome en 1953, son épouse Grace Hubble en donna une image romancée et enjolivée, du genre <<C'était un Olympien, grand, fort et beau, avec les épaules de l'Hermès de Praxitèle, et une douce sérénité>> ! (cité dans Osterbrock et al, Bibliographie générale.) Ceci ne contribua guère à rendre les récits de ses biographes très fidèles.Retour texte
[92] cf. Godart, Odon et Heller, Michael, Lemaître Cosmology, Tucson, Pachart Publishing House, 1985, p. 57.Retour texte
[93] G. Lemaître, <<A homogeneous universe of constant mass and increasing radius accounting for the radial velocity of extra -galactic nebulae>>, Monthly Notices of the Royal Astronomical Society, t. XCI, 1931, pp. 483-490.Retour texte
[94] A.S. Eddington, <<[Remarks at the Meeting of the Royal Astronomical Society]>>, The Observatory, vol. 53, 1930, p. 39-40.Retour texte
[95] A.S. Eddington, The Observatory, vol. 53, 1930, p. 162-164.Retour texte
[96] A.S. Eddington, <<On the Instability of Einstein's Spherical Wolrd>>, Monthly Notices of the Royal Astronomical Society, t. 90, 1930, p. 668-678.Retour texte
[97] G.F. Paddock, <<The Relation of the System of Stars to the Spiral Nebulae>>, Publications of the Astron. Soc. Pacific, 28, pp. 109-115 (1916). C. Wirtz, <<Über die Bewegung der Nebelflecke>>, Astr. Nachr. 206, pp. 109-116 (1918), et <<Notiz zur Radialbewegung der Spiralnebel>>, Astr. Nach. 216, p. 451 (1922).Retour texte
[98] G. Lemaître, <<The expanding universe>>, Monthly Notices of the Royal Astronomical Society, t. XVI, mars 1931 , pp. 483(490) -501.Retour texte
[99] Dans ses notes ajoutées à l'article de O. Godart, <<Monseigneur Lemaître, sa vie, son oeuvre >>.Retour texte
[100] Pour une discussion approfondie: J.-F. Robredo, La contribution de Georges Lemaître à la cosmologie moderne; D. Lambert, <<Monseigneur Georges Lemaître et le débat entre le cosmologie et la foi>>, Revue Théologique de Louvain, 28, 1997, 28-53.Retour texte
[101] A. Einstein, <<Zum kosmologischen Problem der allgemeinen Relativitätstheorie>>, Preussische Akademie der Wissenschaften, Sitzungsberichte, 1931, p. 235-237. Trad. franç. in Einstein, Oeuvres choisies, vol. 3, Relativités II, p. 107-110.Retour texte
[102] A. Einstein, W. de Sitter, <<On the Relation between the Expansion and the Mean Density of the Universe>>, National Academy of Sciences, Proceedings, vol. XVIII, 1932, p. 213-214. Traduit en français sous le titre <<Sur la relation entre l'expansion et la densité moyenne de l'univers>>, dans Relativités II, p. 110-112.Retour texte
[103] H.P. Robertson, <<On the Foundations of Relativistic Cosmology>>, National Academy of Sciences, Proceedings, vol. XV, 1929, p. 822-829.Retour texte
[104] Otto Heckmann, <<Über die Metrik des sich ausdehnenden Universums>>, Nach. Ges. Gött. Wiss. 127-130, 1931.Retour texte
[105] Voir par exemple P. Coles et G. Ellis, <<The case for an open universe>>, Nature, vol. 370, 1994, p. 609.Retour texte
[106] Des limites peuvent être fixées sur l'âge de l'univers à partir de celui des étoiles les plus vieilles de notre galaxie et à partir des abondances de certains éléments radioactifs. Des valeurs de 12 à 17 milliards d'années sont avancées. Voir D. Clayton, <<Cosmology, Cosmochronology>>, in S. Maran (éd.), The Astronomy and Astrophysics Encyclopedia p. 153-156. New York, Van Nostrand Reinhold, 1992.)Retour texte
[107] A.S. Eddington, <<The End of the World : from the Standpoint of Mathematical Physics>>, Nature, vol. 127 pp. 447-453 (21 mars 1931).Retour texte
[108] D. Lambert, <<Monseigneur Georges Lemaître et le débat entre le cosmologie et la foi>>.Retour texte
[109] G. Lemaître, <<L'Univers en expansion>>, Annales de la Société Scientifique de Bruxelles, série A, t. III, 1933, pp. 51-85.Retour texte
[110] cf J. Eisenstaedt, <<Histoire et singularités de la solution de Schwarschild (1915-1923)>>, Archives Hist. Exact Sciences, vol. 27, 1982, p. 157-198.Retour texte
[111] Voir J.-P Luminet, Les trous noirs, Le Seuil/Points Sciences, Paris 1992.Retour texte
[112] Voir par exemple S.W. Hawking et G.F.R. Ellis, The Large Scale Structure of Spacetime. Retour texte
[113] Les rapports entre science et foi religieuse dans la pensée de Lemaître ont été analysés notamment dans O. Godart, <<Contributions of Lemaître to General Relativity (1922-1934)>>, [[section]]7 ; O. Godart et M. Heller, <<Les relations entre la science et la foi chez Georges Lemaître>>, in Commentarii, Académie Pontificale des Sciences, vol. III, ndeg.121, pp.1-12 ; J.F. Robredo, Les idées cosmologiques de Lemaître entre science et religion, rapport de séminaire à l'Observatoire de Meudon, janvier 1993 ; D. Lambert, <<Mgr. Georges Lemaître et les <<Amis de Jésus>>>>, Revue Théologique de Louvain, 27, 1996, 309-343, et <<Monseigneur Georges Lemaître et le débat entre le cosmologie et la foi>>, Revue Théologique de Louvain, 28, 1997, 28-53. Lemaître s'est lui-même exprimé sur la question dans <<La culture catholique et les sciences positives>>, in Actes du VIe congrès catholique de Malines. - Vol. 5, pp. 65-70.Retour texte
[114] Dans O. Godart, <<Monseigneur Lemaître, sa vie, son oeuvre>>, op. cit.Retour texte
[115] G. Lemaître, <<Rencontres avec A. Einstein>>, Revue des Questions Scientifiques, t. LXXIX, 5e série, t. XIX, janvier1958, ndeg.2, pp. 129-132.Retour texte
[116] Dans les notes ajoutées à O. Godart, op. cit.Retour texte
[117] Voir par exemple S. Carroll et W. Press, <<The cosmological constant>>, Ann. Rev. Astron. Astrophys., vol. 30, 1992, p. 499-542.Retour texte
[118] <<L'hypothèse de l'atome primitif>> in Revue des Questions Scientifiques, 61e année, 5e série, t. IX, 1948, pp. 321-339 ; <<L'hypothèse de l'atome primitif>> - texte d'une Conférence du Palais de la découverte, 13 mai 1947 publiée à Alençon chez Poulet-Malassis, 1948.Retour texte
[119] Lui-même auteur d'ouvrages sur l'espace et les géométries non-euclidiennes, par exemple La géométrie et le problème de l'espace, Neuchâtel, Ed. du Griffon.Retour texte
[120] H. Bondi et T. Gold, <<Th Steady State Theory of the Expanding Universe>>, MNRAS, 108, 1948, p. 252-270 ; F. Hoyle, <<A New Model for the Expanding Universe>>, MNRAS, vol. 108, 1948, p.372-382.Retour texte
[121] Observateurs et théoriciens se mirent d'accord sur une publication simultanée de leurs résultats respectifs en deux notes distinctes mais consécutives. Dans R.H. Dicke, P.J.E. Peebles, P. G. Roll et D. T. Wilkinson, <<Cosmic Black Body Radiation>>, The Astrophysical Journal, vol. 142 (1965) 414-418, le groupe de Princeton justifiait les conclusions cosmologques qu'ils tiraient de lettre de Penzias et Wilson qui suivait : <<Measurement of Excess Antenna Temperature at 4800 Mc/s>>, The Astrophysical Journal, vol. 142, 419-423. Au début des années 1990, les données recueillies par le satellite COBE en ondes millimétriques ont permis de fixer la température du rayonnement cosmologique avec une grande précision : 2,736 +/- 0,017 degrés Kelvin. Voir par exemple Marc Lachièze-Rey et Edgar Gunzig, Le Fond Diffus Cosmologique, Paris, Masson, 1995.Retour texte
[122] Voir par exemple E. Harrison, Le noir de la nuit, Seuil/Science ouverte, 1990 ; J.-P. Luminet et M. Lachièze-Rey, La physique et l'infini, Flammarion/Dominos, Paris, 1994. Retour texte
[123] Communication privée de Jacques Merleau-Ponty. L'auteur remercie J. Frieben pour la traduction.Retour texte
[124] Ibid.Retour texte
[125] Allusion à l'<<hypertore>>, variante de l'espace Euclidien à trois dimensions obtenue en considérant comme identiques tous les points appartenant aux faces opposées d'un parallélépipède. Voir Lachièze-Rey, M. et Luminet, J.-P. : <<Cosmic Topology>>, Physics Reports, vol. 254, 1995, pp. 135-214.Retour texte
[126] Lachièze-Rey, M. et Luminet, J.-P. : <<Cosmic Topology>>, op.cit., [[section]]7.Retour texte
[127] E. Feodoroff, <<Symmetrie der regelmassigen Systeme der Figuren>>, Russian journal for crystallography and mineralogy, St Petersburg, vol. 21, 1885 ; L. Bierbach, <<Über die Bewegungsgruppen der Euklidischen Raume I>>, Mathematische Annalen, vol. 70, 1911, pp. 297-336. II, ibid vol. 72, 1912, pp. 400-412Retour texte
[128] W. Novacki, <<Die euklidishen, dreidimensionalen, geschlossenen und offenen Raumformen>>, Commentarii Mathematici Helvetici, vol. 7, 1934, pp.81-93.Retour texte
[129] F. Klein, <<Zur nicht-euklidischen Geometrie>>, Mathematisches Annalen, vol. 37, 1890, p. 544 ; W. Killing, <<Über die Clifford-Kleinschen Raumformen, Mathematisches Annalen, vol. 39, 1891, p. 257.Retour texte
[130] J.A. Wolf, <<Sur la classification des variétés riemanniennes homogènes à courbure constane>>, Comptes rendus de l'Académie des Sciences de Paris, vol. 250, 1960, pp. 3443-3445.Retour texte
[131] W. Thurston, The geometry and topology of three manifolds, Princeton Lecture Notes, 1979.Retour texte
[132] Dont le texte a été publié à titre posthume dans <<L'Univers, problème accessible à la science humaine>>, Revue d'Histoire Scientifique, t. 31, 1978, pp. 345-359.Retour texte
[133] Lemaître, G. : La structure et l'évolution de l'univers, Onzième Conseil de Physique Solvay, 1958.Retour texte
[134] Cf. références dans Lachièze-Rey, M. et Luminet, J.-P. : <<Cosmic Topology>>.Retour texte
[135] Lehoucq R., Lachièze-Rey M. & Luminet J.-P., <<Cosmic Crystallography>>, Astronomy and Astrophysics, vol. 313, 1996, pp. 339-346Retour texte
Encadré 1 : Représentation mathématique
des univers de Friedmann - Lemaître
1.1 Les équations du champ
En relativité générale, l'espace-temps
est décrit au moyen d'une variété
pseudo-riemannienne à quatre dimensions,
caractérisée localement par un tenseur métrique
![]() tel que l'intervalle
ds entre deux points voisins est
tel que l'intervalle
ds entre deux points voisins est
![]() .
.
Les propriétés géométriques de
l'espace-temps sont liées à la distribution de masse et
d'énergie, donnée par le tenseur
impulsion-énergie ![]() ,
selon les équations du champ d'Einstein
,
selon les équations du champ d'Einstein
![]() (1)
(1)
où ![]() est le tenseur
de courbure de Ricci,
est le tenseur
de courbure de Ricci, ![]() est
sa contraction,
est
sa contraction, ![]() est la
constante cosmologique, et
est la
constante cosmologique, et
![]()
1.2 Les simplifications cosmologiques.
L'application des équations de la relativité générale à la description de la structure de l'univers autorise deux simplifications importantes, qui permetttent de trouver des solutions exactes :
1/ L'univers est empli d'un fluide parfait de densité ![]() et de pression
et de pression ![]() , dont le tenseur
impulsion-énergie s'écrit
, dont le tenseur
impulsion-énergie s'écrit
![]() (2)
(2)
où ![]() sont les
composantes du quadrivecteur-vitesse du fluide. En choisissant
convenablement les coordonnées (comobiles), les seules
composantes non-nulles de (2) sont
sont les
composantes du quadrivecteur-vitesse du fluide. En choisissant
convenablement les coordonnées (comobiles), les seules
composantes non-nulles de (2) sont
![]()
Une simplification supplémentaire sur
l'équation d'état de la matière consiste
à supposer que la pression ![]() est nulle (approximation dite "poussière").
est nulle (approximation dite "poussière").
2/ A grande échelle, on peut également supposer que la matière cosmique est distribuée de façon homogène (densité constante dans l'espace) et isotrope (indépendante de la direction).
Il s'ensuit que l'espace est à courbure constante, et que l'élément de métrique prend la forme dite de Friedmann-Lemaître- Robertson - Walker (FLRW) :
![]() (3)
(3)
où ![]() sont des coordonnées sphériques, la constante
k est égale à +1, 0 ou -1 selon que la courbure
est positive (espace elliptique), nulle (espace euclidien) ou
négative (espace hyperbolique).
sont des coordonnées sphériques, la constante
k est égale à +1, 0 ou -1 selon que la courbure
est positive (espace elliptique), nulle (espace euclidien) ou
négative (espace hyperbolique). ![]() représente la courbure de l'espace,
représente la courbure de l'espace, ![]() étant une quantité
sans dimension fonction du temps, appelée initialement rayon
d'univers et rebaptisée plus correctement facteur
d'échelle, dans la mesure où elle ne
représente pas le rayon physique de l'espace (qui peut
être infini).
étant une quantité
sans dimension fonction du temps, appelée initialement rayon
d'univers et rebaptisée plus correctement facteur
d'échelle, dans la mesure où elle ne
représente pas le rayon physique de l'espace (qui peut
être infini).
Une forme équivalente de (3) est
 (4)
(4)
1.3 Les équations de Friedmann-Lemaître
Le problème cosmologique se réduit alors
à déterminer les trois fonctions inconnues ![]() , constantes dans l'espace mais
a priori variables dans le temps, à partir des
équations du champ (1).
, constantes dans l'espace mais
a priori variables dans le temps, à partir des
équations du champ (1).
Pour déterminer![]() ,
il faut trois relations indépendantes. Les équations du
champ permettent d'en fixer deux, sous forme d'équations
différentielles ordinaires :
,
il faut trois relations indépendantes. Les équations du
champ permettent d'en fixer deux, sous forme d'équations
différentielles ordinaires :
![]() (5a)
(5a)
![]() (5b)
(5b)
Une combinaison astucieuse des deux relations (5) permet de retrouver la loi de conservation de l'énergie :
![]() (6)
(6)
La troisième relation doit être
spécifiée indépendamment des équations
d'Einstein ; c'est l'équation d'état du fluide : ![]() .
.
Le rapport ![]() , qui mesure
le taux de variation du facteur d'échelle (taux d'expansion si
R(t) croît), est appelé paramètre de Hubble. Sa
valeur aujourd'hui,
, qui mesure
le taux de variation du facteur d'échelle (taux d'expansion si
R(t) croît), est appelé paramètre de Hubble. Sa
valeur aujourd'hui, ![]() , est
la constante de proportionnalité entre le décalage
spectral des galaxies lointaines et leur distance.
, est
la constante de proportionnalité entre le décalage
spectral des galaxies lointaines et leur distance.
1.4 Les solutions cosmologiques
Univers cylindrique d'Einstein (1917)
R(t) = constante = R et k = +1 dans (3), p=0,
![]()
Univers sphérique de de Sitter (1917)
La solution donnée originellement par de Sitter est
![]()
avec
p=0, ![]()
Par le changement de coordonnées
![]()
introduit par Lemaître, la métrique réécrite sous la forme (3) devient :
![]()
Sous cette forme, l'espace apparaît euclidien (k = 0)
Univers sphérique de Friedmann (1922)
k = +1 dans (3), p = 0,
L quelconque.L'évolution temporelle du facteur d'échelle R(t) dépend de la constante cosmologique, voir Tableau 1 ligne 3.
Univers hyperbolique de Friedmann (1924)
k = - 1 dans (3), p = 0,
L quelconque.L'évolution temporelle du facteur d'échelle R(t) dépend de la constante cosmologique, voir Tableau 1 ligne 1.
Univers sphérique de Lemaître-Eddington (1927)
k =+1, p _0,
L = LEEvolution temporelle du facteur d'échelle : Figure 1.
Univers hésitant de Lemaître (1931)
k =+1,
L > LEEvolution temporelle du facteur d'échelle : Figure 2.
Univers euclidien d'Einstein-de Sitter (1932)
k = 0,
L=0, p = 0![]() ,
,
![]()
où R0 et H0 sont les valeurs actuelles du facteur d'échelle R(t) et du paramètre de Hubble H(t).
Table 1 : Représentation graphique
des univers de Friedmann - Lemaître
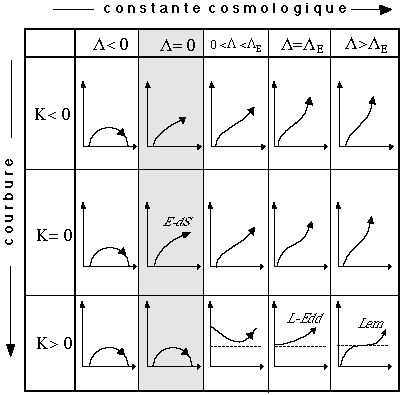
La dynamique des modèles cosmologiques de Friedmann - Lemaître, c'est-à-dire la variation du facteur d'échelle spatiale en fonction du temps cosmique, est déterminée par le signe de la courbure (constante) des sections spatiales, k, et par la valeur de la constante cosmologique,
L. Deux valeurs critiques de cette constante sont L = 0 (on retrouve alors les modèles de Friedmann les plus souvent utilisés, dans la colonne en gris; un cas particulier est la solution euclidienne d'Einstein - de Sitter, marquée E-dS), et L = LE, où LE est la valeur proposée en 1917 par Einstein afin d'assurer la staticité de son univers sphérique. Puisqu'une constante cosmologique positive équivaut à une action répulsive à grande distance, tous les modèles à grande constante cosmologique (L > LE), quelle que soit leur courbure, sont "ouverts" dans le temps, c'est-à-dire en expansion perpétuelle. A l'inverse, une constante négative (L <0) contribue à augmenter la gravité effective, de sorte que les modèles d'univers correspondants finissent tous par s'effondrer sur eux-mêmes.Dans certains cas (k>0 et 0 <
L < LE), la singularité initiale peut disparaître; en particulier, le modèle de Lemaître-Eddington (marqué L-Edd) est un univers spatialement fermé en expansion continue à partir de la sphère statique d'Einstein (correspondant à un rayon constant indiqué en pointillés). Le modèle à explosion primordiale prôné par Lemaître (marqué Lem) a une constante cosmologique légèrement supérieure à la valeur critique LE, de sorte qu'il traverse une phase plus ou moins longue au cours de laquelle il frôle l'état statique d'Einstein, avant de repartir en expansion continûment accélérée.
1915 : Einstein et Hilbert donnent les équations définitives de la théorie de la relativité générale.
1917 : Einstein dérive le premier modèle cosmologique relativiste. L'espace est sphérique, statique, de densité uniforme. Einstein introduit la constante cosmologique.
1917 : De Sitter dérive le second modèle cosmologique relativiste. L'espace est statique, vide de matière.
1918 : Weyl expose ses idées sur l'unification possible de la gravitation et de l'électromagnétisme.
1920: Shapley et Curtis participent au <<grand débat>> sur la nature extragalactique des nébuleuses.
1922 : Friedmann fournit le premier modèle d'univers en expansion, à courbure et densité positives, constante cosmologique non nulle et pression nulle.
1922 : Einstein prétend que Friedmann a fait une erreur de calcul.
1923 : Einstein retire sa critique et admet son erreur.
1923 : Friedmann publie L'Univers comme Espace et Temps.
1923: Weyl suggère le caractère non statique de l'univers de de Sitter
1924 : Friedmann donne le premier modèle d'univers en expansion hyperbolique. Première discussion d'envergure sur la topologie cosmique.
1924 : Eddington indique que sur 41 décalages spectraux de galaxies mesurés, 36 sont vers le rouge ; il favorise la solution de de Sitter.
1925 : Lemaître trouve une seconde forme de la métrique de de Sitter, suggérant un espace en expansion de courbure nulle.
1925 : Lemaître démontre une relation linéaire entre la distance et le décalage spectral dans la solution de de Sitter.
1925 : Hubble établit l'échelle de distances extragalactiques et clôt le <<grand débat>>.
1927 : Lemaître propose un modèle d'univers en expansion à courbure et constante cosmolgique positives, applique les lois de conservation de l'énergie et les équations du champ avec pression. Il donne la première interprétation des décalages vers le rouge liée à l'expansion de l'univers et prédit la relation linéaire distance-décalage vers le rouge.
1929 : Robertson trouve la métrique générale pour tous les univers spatialement homogènes, mais ne réalise pas leur importance.
1929 : Hubble trouve expérimentalement la relation linéaire distance-décalage vers le rouge, mais ne la relie pas à l'expansion.
1930 : Eddington prouve l'instabilité de l'univers d'Einstein et adopte le modèle de Lemaître.
1931 : Hubble et Humason fixent la constante de proportionnalité entre vitesse de récession et distance à Ho = 558 km/s/Mpc.
1931 : Lemaître propose son modèle d'univers initialement singulier, l'atome primitif, dans lequel une phase de stagnation permet la formation des galaxies. Il suggère que les rayons cosmiques sont les reliques de l'univers primitif.
1931 : Lemaître propose une origine quantique de l'univers.
1932 : Einstein et de Sitter analysent le cas le plus simple à courbure, pression et constante cosmologique nulles; ils donnent la relation entre la densité et le taux d'expansion.
1945 : Lemaître réunit son oeuvre cosmologique dans L'hypothèse de l'atome primitif.
1946 : Gamow propose la nucléosynthèse cosmologique.
1948 : Alpher, Bethe et Gamow calculent les abondances des éléments formés dans l'univers primitif.
1949 : Alpher et Herman font la prédiction d'un fond diffus cosmologique, sous forme de rayonnement de corps noir à la température de 5 degrés Kelvin.
1952 : Baade révise l'échelle de distances extragalactiques, qui augmente l'échelle de temps cosmique d'un facteur 2,6.
1965 : Penzias et Wilson découvrent un fond diffus de rayonnement radio à la température de 3 degrés Kelvin. Dicke et Peebles en donnent l'interprétation cosmologique dans le cadre des modèles de Big Bang.
1992 : Le satellite d'observation COBE vérifie la nature thermique, l'homogénéité et l'isotropie du fond diffus cosmologique à une précision de 10-5, et décèle les premières fluctuations de densité.