


Par la hardiesse de ses idées, la cosmologie a toujours suscité passions et controverses. Les nouvelles théories du Big Bang posent des questions plus déroutantes que jamais : l'Univers est-il un jeu de miroirs ou une écume d'espace-temps ?
En tentant d'intégrer les spéculations les plus avancées de la physique théorique, le débat cosmologique connaît aujourd'hui une vivacité sans précédent. Toutefois il ne trouve sa véritable portée qu'en s'interrogeant aussi sur sa propre histoire. La mise en perspective épistémologique d'une discipline permet en effet d'en relativiser les affirmations contemporaines, provisoires comme c'est de règle en science, mais que d'aucuns auraient tendance à considérer comme définitives.
Nombre de cosmologistes modernes ignorent que, par le seul fait de pratiquer leur discipline, ils adoptent une position philosophique : ils admettent implicitement que l'univers est beau et ordonné. L'étymologie même du mot "cosmologie" l'indique : en grec, le kosmos désignait la parure des femmes, les ornements, le bel aspect physique ou moral (à rapprocher du latin mundus, qui a donné l'adjectif "mondain"). La notion de cosmos appliquée à l'organisation de l'univers apparaît ainsi vers le VIe siècle avant notre ère chez les Milésiens (Thalès, Anaximandre et autres physiciens de la ville de Milet, en Asie mineure) : la réalité n'est pas le chaos que décrivait Hésiode dans sa "Théogonie" , deux siècles plus tôt ; elle est au contraire belle et arrangée.
Par ailleurs le mot Univers, synonyme de Cosmos mais issu du latin, contient les notions d'Unité et de Diversité. C'est bien le propos de la cosmologie que d'expliquer par une unité sous-jacente l'extraordinaire diversité observée dans le monde matériel - des particules élémentaires jusqu'aux superamas de galaxies.
Curieusement, le terme de cosmologie n'est apparu qu'en 1731, dans l'ouvrage intitulé Cosmologia Generalis du baron allemand Christian Wolff, disciple de Leibniz : depuis deux millénaires et demi il existait donc un discours sur l'univers qui n'avait pas de nom! Wolff, comme la plupart de ses prédécesseurs, s'efforça d'aborder les questions sur la nature physique du monde en se dégageant le plus possible du mythe et de la religion.

|
ESSAI DE COSMOLOGIE
La première apparition en français du mot "cosmologie" figure dans "L'essai de Cosmologie" de Pierre-Louis Moreau de Maupertuis (1698-1759), paru en 1750. Ce dernier fit preuve de génie aussi bien en physique qu'en mathématiques et en astronomie. Il dirigea notamment une expédition en Laponie destinée à mesurer la figure de la Terre.
|
Or, une curiosité épistémologique omniprésente dans toute l'histoire de la cosmologie est le procès quasi-permanent qui lui a été intenté (parfois à juste titre, parfois injustement) d'interpénétrer les principes philosophico-religieux et les énoncés physiques. Par exemple, si le terme de "cosmologie" est consacré en 1752, dans un article de l`Encyclopédie par Jean le Rond d'Alembert , ce dernier ne se prive pas de remarquer que le sujet n'est guère digne d'intérêt, car il se réduit aux questions de savoir si l'on peut trouver Dieu dans la nature ! Pour de nombreux physiciens, la cosmologie voisinait avec le rêve et l'extase. Les récits "cosmologiques" tels ceux de Platon, Cicéron, Dante ou Cyrano, mettaient en jeu des êtres "exceptionnels" (parler de l'univers comme une totalité, c'est comme se placer extérieur à lui), capables de raconter leur expérience de l'inexpérimentable. Ceci n'est pas sans rappeler les récits de "near-death expériences" en vogue aujourd'hui.
Il est vrai que, jusqu'au début du XXe siècle, les considérations sur l'univers n'étaient étayées par aucune observation proprement cosmologique, de sorte que les modèles étaient plaqués sur des présupposés philosophiques et religieux. Ne croyons pas pour autant que cette interpénétration de la physique et de la philosophie ait cessé : Albert Einstein, l'inventeur de la théorie de la relativité générale, qui sert de base à toutes les études cosmologiques actuelles, s'y est le premier laissé prendre ; parmi les solutions possibles de ses équations, il choisit pour des raisons esthétiques celle qui décrivait un univers statique et fini. De même, on ne peut pas démontrer le "principe cosmologique" qui sous-tend tous les modèles actuels d'univers et stipule qu'il n'existe aucune position privilégiée dans l'espace.
A côté de ces justes critiques, de faux procès sont intentés à la cosmologie. L'un d'entre eux a injustement gâché la renommée scientifique du plus grand cosmologiste de ce siècle : Georges Lemaître, inventeur du concept de big bang avec le russe Alexandre Friedmann. On lui a reproché de vouloir confirmer par la science le récit de la Genèse. Il n'en était rien : abbé, certes, mais brillant scientifique, Lemaître tenait à une distinction radicale entre science et religion, pensant que l'on ne pourra jamais réduire l'Être suprême au rang d'une hypothèse scientifique - comme le disait à Napoléon le mathématicien français Pierre Simon de Laplace. Cependant Lemaître joua de malchance : le 22 novembre 1951, le pape Pie XII déclarait devant l'Académie Pontificale : "Il semble en vérité que la science d'aujourd'hui, remontant d'un trait des millions de siècles, ait réussi à se faire le témoin de ce Fiat Lux initial. Vers cette époque, le cosmos est sorti de la main du Créateur".
Farouche adversaire d'un tel "concordisme", Lemaître demanda audience au pape et remit respectueusement les choses en place. Le 7 septembre 1953, devant l'assemblée générale de l'Union Astronomique Internationale, Pie XII tint effectivement un discours radicalement opposé : la cosmologie scientifique ne parlait ni de Fiat lux , ni de création.
Un autre mauvais procès intenté à la cosmologie est qu'elle ne serait pas assez fondée sur le témoignage des sens. Pourtant, cette caractéristique n'a nullement empêché Copernic de fonder sa nouvelle hypothèse sur une vision purement esthétique de l'univers, en faisant fi des erreurs dont étaient entachées les tables d'observation astronomiques ("Je ne peux qu'admirer ceux qui ont opté pour l'héliocentrisme en dépit du témoignage de leurs sens", dit plus tard Galilée). Et Johannes Kepler de découvrir l'ellipticité des orbites planétaires en se fondant sur la croyance en l'harmonie des sphères.
Remarquons que nombre d'assertions cosmologiques prêtent, aujourd'hui encore, le flanc à de telles critiques. On lit partout que le "Big Bang" est la violente explosion qui a donné naissance à l'Univers. Tout est faux dans une telle proposition, qui confond le début de l'univers (qui échappe à la description scientifique) et le début de l'intelligibilité de l'univers. Pis encore, lors de la découverte des fluctuations du rayonnement cosmologique en 1993, on a entendu d'éminents cosmologistes déclarer : "Si vous êtes croyant, c'est comme si vous voyez la face de Dieu", "Le Saint Graâl de la physique", " La plus grande découverte de tous les temps".... De tels rapprochements entre cosmologie et croyance, ou entre science et spectacle, ne sont pas de nature à clarifier les idées du public. Faut-il y voir une concession à l'étonnante médiatisation de la discipline, c'est-à-dire à une certaine rouerie, ou au contraire le signe d'une grande naïveté ?
Pour finir, les adversaires de la cosmologie font valoir qu'il n'existe même pas de bonne définition de l'univers. C'est exact, mais pour paraphraser le physicien américain Richard Feynman, les cosmologistes sont bien décidés à explorer le monde sans en avoir de définition !
La cosmologie moderne
Quel est donc l'état actuel de la cosmologie ? L'univers est décrit par une structure spatio-temporelle munie d'un contenu matériel (matière et rayonnement), dont le couplage et la dynamique sont régis par la théorie de la relativité générale. Ce cadre formel permet de concevoir une grande variété de modèles d'univers, dont les prédictions doivent être confrontées aux observations. Les astrophysiciens retiennent les solutions qui décrivent un univers homogène (c'est-à-dire avec de la matière uniformément répartie dans tout l'espace), en expansion depuis une singularité initiale remontant à une quinzaine de milliards d'années. Ce sont les modèles standard de big bang. Le terme "standard" signifie que des simplifications supplémentaires sont supposées : ne sont pas prises en compte la constante cosmologique (qui décrit une sorte de répulsion s'exerçant à l'échelle de l'univers lui-même), les complications topologiques de l'espace-temps ni ses propriétés quantiques. Malgré leur grande simplicité, les modèles standard de big bang fournissent une excellente description de l'univers durant une grande partie de son évolution, expliquant le noir du ciel, le décalage vers le rouge des galaxies, la proportion des éléments chimiques légers, le nombre d'espèces différentes de neutrinos, l'existence d'un rayonnement diffus de corps noir à la température de 2,73 Kelvins uniformément réparti sur le fond de ciel, et les petites irrégularités observées dans ce rayonnement.
Parmi les questions qui restent inexpliquées par les modèles standard de big bang, certaines sont de détail, d'autres de fond. Les questions de détail (sans aucune connotation péjorative) sont celles dont la résolution ne devrait impliquer qu'un approfondissement ou des aménagements mineurs de la théorie de base, la relativité générale. Par exemple, il est d'usage de penser que les questions mal comprises sur la matière sombre, la formation des galaxies, la quasi-absence d'antimatière ou la quasi-parfaite uniformité de la répartition de la matière à grande échelle devraient se résoudre par la physique des particules de haute énergie appliquée à l'Univers primitif.
Les études des brisures de symétrie, de l'apparition de défauts topologiques tels que cordes, murs ou textures cosmiques, et de la fameuse inflation - brève période pendant laquelle les dimensions de l'Univers primitif auraient augmenté dans des proportions gigantesques - relèvent de cette ligne de raisonnement.
Il est d'ailleurs intéressant de retracer le bref historique du concept d'inflation. Je me souviens d'avoir entendu le physicien belge François Englert l'introduire pour la première fois à l'École de Cosmologie des Houches en 1979, mais ce n'est qu'en 1981 que l'idée a subitement fait fortune, avec un article de l'Américain Alan Guth. Il est vrai que le lieu de publication était mieux trouvé, ainsi que le "bon" mot d'inflation (on n'insistera jamais assez sur le pouvoir des mots : le terme de Big Bang est devenu célèbre du jour au lendemain, à la suite d'une émission de la radio britannique où il avait été utilisé de façon ironique par l'un de ses adversaires acharnés, Fred Hoyle). Comme l'idée était séduisante, des centaines de cosmologistes se sont mis à la peaufiner et à construire des modèles. Les effets de mode sont d'autant plus importants que le statut social du jeune chercheur est précaire, le renouvellement des contrats de recherche post-doctorale dans les pays anglo-saxons obligeant à une rapidité de résultats sur des sujets réputés "pointus". Qu'observe-t-on 15 ans après ? Des retouches de plus en plus compliquées et invraisemblables apportées successivement aux modèles d'inflation pour "sauver les apparences". Cela ne rappelle irrésistiblement l'introduction de l'équant par Ptolémée dans la théorie des épicycles...
L'univers, fini ou infini?
Les questions de fond posées par les modèles standard de big bang concernent la singularité initiale (en mathématiques, une singularité est un point où certaines quantités deviennent infinies ; ici la courbure, la température, la densité d'énergie, etc.) et la topologie de l'espace-temps. Elles mettent sans doute en jeu la validité même de la relativité générale. En effet, en tant que singularité d'une théorie non quantique, le Big Bang serait une limite absolue à la compréhension du début de l'Univers, puisque les lois de la physique s'y sont plus valables, ni même les concepts les plus élémentaires d'espace et de temps. Quant à la topologie de l'univers (l'espace est-il fini ou infini, orienté ou non ?), la relativité générale n'en rend même pas compte, puisqu'elle ne permet de traiter que des propriétés géométriques locales de l'univers, et non des caractéristiques globales.
A bien y regarder, ces deux questions sont liées à celles de l'infini. La cosmologie est le royaume privilégié des infinis : infinis de l'espace, du temps passé et du temps futur ; infinis, grands ou petits, de température, de pression, d'énergie, de dimensions, liés à la singularité initiale. Les premiers sont discutés depuis trois millénaires, les seconds sont apparus avec la théorie de la relativité générale (aussi bien dans les modèles de big bang que dans ceux d'effondrement gravitationnel conduisant aux fameux "trous noirs").
Commençons par les premiers. L'histoire de la cosmologie tourne sans cesse autour de la lancinante question : l'espace est-il fini ou infini ? Au VIe siècle avant notre ère règne l'idée d'un Monde (terre, planètes, étoiles) fini, entouré d'un milieu infini. Puis, au IVe siècle, Platon postule dans son dialogue intitulé le Timée que le monde et les cieux étaient tous deux finis, enclos dans une série sphère. Le souci premier de sa modélisation cosmologique est celui d'harmonie et de symétrie maximale (la sphère étant la figure parfaite par excellence, elle doit naturellement s'inscrire dans l'architecture cosmique pour refléter la perfection et l'immuabilité divines). Vient alors Aristote, qui élimine l'infini de toute la physique, avec une influence qui durera deux millénaires. En passant de l'infini au fini et en identifiant le monde physique à un espace géométrique, les aristotéliciens accomplissent la première étape clef de la modélisation cosmologique.
Le XVIIe siècle voit une évolution opposée: les sphères aristotéliciennes éclatent après les observations de Tycho-Brahé et de Galilée, après les considérations métaphysiques de Giordano Bruno, après l'ouvrage de vulgarisation de Thomas Digges et après les ellipses du génial Kepler. C'est le passage du monde clos à l'Univers infini. Cette nouvelle vision cosmologique est consacrée par Newton, qui identifie désormais l'Univers à l'espace euclidien infini.
Ce passage est important : chez les Milésiens, le monde était considéré comme étant dans l'espace - par exemple un cosmos enclos dans le volume d'une sphère, elle-même plongée dans un espace extra-cosmique infini, sans propriété physique. Chez les Aristotéliciens, le monde s'identifie à l'espace, et il est fini. Avec les atomistes et avec Newton, monde et espace coïncident et sont infinis.
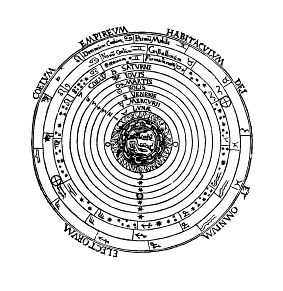
|
La nature de l'espace fut découverte progressivement. L'idée d'un
monde fini, borné par une ultime sphère où auraient
été accrochées les étoiles fixes, se maintint
jusqu'au temps de Nicolas Copernic.
|
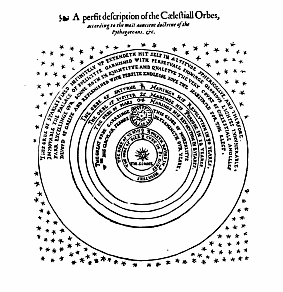
|
Au début du XVIIe siècle, une nouvelle vision du monde s'instaura; on en vint à penser que les étoiles se répartissaient dans un espace infini. Le terrain était prêt pour Isaac Newton, qui identifia l'Univers à l'espace euclidien infini.
|
Troisième étape clef : au début du XXe siècle, la théorie de la relativité générale offre un nouveau cadre de compréhension de l'Univers en termes d'un espace-temps courbé par la matière : si notre univers n'avait qu'une dimension d'espace et une dimension de temps, il serait analogue à un feuillet de courbure variable selon la répartition des masses ; toutefois ce feuillet ,ne serait pas plongé dans l'espace à trois dimensions que nous connaissons, puisque rien n'existe en dehors de l'Univers.
Dans les modèles cosmologiques relativistes, l'Univers s'identifie à une entité physico-géométrique : l'espace-temps-matière. Remarquons que l'identification du monde physique et de l'espace (ou de l'espace-temps) géométrique reste mal comprise du public. Lorsqu'un conférencier parle de l'expansion de l'Univers, il se voit invariablement poser la question : dans quoi l'Univers gonfle-t-il? Cette formulation incorrecte est sans doute accentuée par l'analogie trop souvent employée entre l'Univers en expansion et la surface d'un ballon que l'on gonfle. En fait, l'Univers ne gonfle dans rien, puisqu'il n'existe pas d'espace en dehors de lui. On ignore souvent, tout comme les Grecs d'il y a deux mille ans, que les mathématiques savent décrire des espaces non euclidiens parfaitement finis (un vaisseau spatial filant droit devant lui reviendrait à son point de départ), mais n'ayant nul besoin d'un espace référent extérieur. De même, le temps, qui est une propriété de l'Univers au même titre que l'espace, n'a pas de référent extérieur, de sorte que l'autre question souvent posée : qu'y avait-il avant le Big Bang, est également incorrecte. Vers 1230, le philosophe Guillaume d'Auvergne l'avait remarquablement exprimé : "De même que le Monde n'a pas de dehors, n'a pas d'au-delà, puisqu'il contient et embrasse toute chose, de même le temps, qui a commencé à la création du Monde, n'a pas d'auparavant ni de précédemment, puisqu'il contient en lui tous les temps qui sont ses parties."
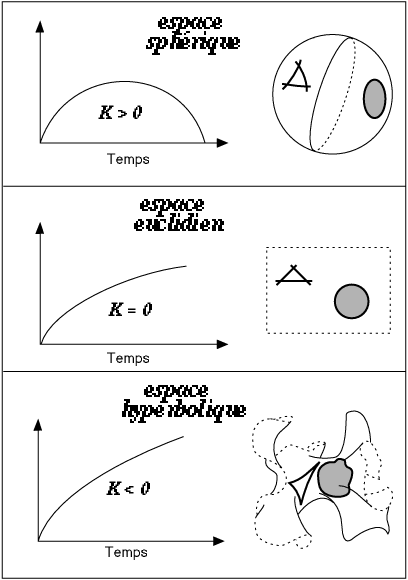
La cosmologie relativiste fait appel aux géométries non-euclidiennes, si bien que, désormais, les deux possibilités d'espace fini ou infini sont envisageables. En effet, les modèles de Big Bang indiquent que l'espace est soit sphérique (de courbure positive), soit hyperbolique (de courbure négative), soit euclidien (de courbure moyenne nulle). Dans le premier cas, des astronomes qui mesureraient la somme des angles de très grands triangles, dans l'espace, trouveraient une valeur supérieure à 180 degrés; dans le deuxième cas cette somme serait inférieure, -à 180 degrés, et c'est seulement dans le troisième cas qu'ils trouveraient la valeur de 180 degrés que nous mesurons sur les feuilles de papier.
La différence se joue dans la quantité moyenne de matière contenue dans l'Univers - puisque, en relativité générale, la matière détermine la géométrie de l'espace-temps. Au-dessous d'un certain seuil critique de densité, l'espace est hyperbolique, au-dessus il est sphérique; c'est seulement à la valeur exacte de la densité critique que l'Univers est euclidien.
|
La géometrie de l'univers
Les modèles d'Univers de A.Friedmann et G.Lemaître se distinguent par les propriétés de l'espace (telle la courbure) et l'évolution temporelle de l'Univers (expansion ou contraction). Les propriétés de l'espace sont de trois types : modèles à courbure positive, telle l'hypersphère à trois dimensions (a), modèle euclidien, où la courbure est nulle et où la somme des angles de tout triangle est égale à 180 degrés (b), et modèles à courbure négative, telle une nappe plissée où chaque point serait analogue à une selle de cheval (c). Dans les versions les plus simples de ces modèles, l'évolution temporelle de l'Univers est directement liée à la courbure de l'espace : l'Univers est fermé si la courbure est positive, ouvert si la courbure est négative ou nulle.
|
Les conséquences sur la dynamique cosmique sont considérables : si l'espace est sphérique, l'Univers est spatialement fini et temporellement "fermé" : après la phase actuelle d'expansion il se contractera et son histoire s'achèvera par l'opposé d'un Big Bang nommé Big Crunch. Si l'Univers est euclidien ou hyperbolique, il est temporellement "ouvert" : son expansion se poursuivra éternellement. Cependant on ne sait plus, dans ce cas, si l'espace est fini ou infini, car la question de la finitude ou de l'infinitude de l'espace relève non plus de la relativité générale, mais de la topologie, comme nous allons voir.
L'illusion de l'infini
Tout d'abord, insistons sur le fait que l'infinitude spatiale de l'Univers pose quelques problèmes non seulement physiques, mais aussi métaphysiques. Parmi ces derniers, mentionnons brièvement un raisonnement déjà tenu par Epicure au IVe siècle avant notre ère. : si les agents de la causalité (pour Epicure, les atomes) sont en nombre infini, il en est de même de leurs combinaisons, des mondes et de leur diversité. Donc, s'il existe un nombre infini de galaxies, toutes les combinaisons possibles présidant à la naissance et à l'existence d'un être vivant doivent se produire un nombre infini de fois : il existe non seulement une infinité de mondes, mais aussi une infinité d'individus ayant la même structure génétique et la même histoire que n'importe quel individu de notre Terre - vous ou moi.
Comment se débarrasser de l'infini spatial dans les modèles de Big Bang ? L'une des solutions possibles réside dans des considérations de topologie appliquées à l'espace-temps. La topologie est la branche de la géométrie qui classifie les espaces d'après leur forme, leur caractère fini ou infini, etc. On se souvient que les modèles de big bang ont des espaces de type sphérique, euclidien ou hyperbolique selon que leur courbure est positive, nulle ou négative. Leur topologie est usuellement supposée la même que celles des espaces "prototypes" : hypersphère, espace euclidien, hyperboloïde (à trois dimensions), la première étant finie et les deux autres infinies. Cependant il n'y a pas de raison particulière pour que l'espace ait une topologie aussi simple. En tous cas, la relativité générale ne stipule rien à ce propos ; ce n'est que l'application stricte du principe cosmologique, surajouté à la théorie, qui incite à généraliser les propriétés observées localement à la totalité de l'Univers. Ce faisant, on se met dans la position de la fourmi qui, au milieu du désert, est persuadée que le monde entier est composé de grains de sable.
Ainsi un certain nombre de "variantes" topologiques des espaces à trois dimensions peuvent être appliquées à la description de l'espace réel. Pour les univers à courbure positive, elles sont toutes fermées. La situation est bien différente pour les univers à courbure négative ou nulle (favorisés par les observations actuelles, qui indiquent que la densité de matière est inférieure au seuil critique).
Sur les 18 topologies euclidiennes, six sont fermées et orientables (à deux dimensions, un plan est orientable : il possède deux faces distinctes ; un ruban de Möbius n'est pas orientable : il n'a qu'une face). C'est notamment le cas de l'"hypertore" : l'espace défini par l'intérieur d'un cube ordinaire dont on considère que les faces opposées deux à deux sont identiques. Dans cette topologie, l'espace reste euclidien mais acquiert un volume fini.
Quant aux solutions hyperboliques, il en existe une infinité, dont certaines sont fermées. L'une des plus intéressantes est représentable par l'un des polyèdres réguliers, l'icosaèdre, où l'on identifie d'une certaine façon toutes les faces deux à deux; l'espace intérieur, fini, devient "chiffonné" et à courbure négative.

|
Un espace hyperbolique compact. Modèle d'un espace chiffonné hyperbolique. L'intérieur de cet icosaèdre dont les faces de même couleur sont identifiées est un espace fermé de courbure négative (sur la figure, certaines faces visibles à l'avant sont identifiées à des faces cachées à l'arrière). L'espace réel pourrait être de cette nature. C'est l'une des possibilités qu'explorent les cosmologistes aujourd'hui.
|
Avec ces possibilités de "fermeture" topologique de l'Univers disparaît une croyance récente de la cosmologie moderne, selon laquelle, pour savoir si l'espace est fini ou infini, il suffirait de mesurer la quantité de matière qu'il contient. On voit simultanément réapparaître, par le détour de mathématiques sophistiquées, un mythe ancien : l'usage des corps parfaits platoniciens pour expliquer l'architecture secrète du monde !
Ces considérations apportent également un nouvel éclairage sur les rapports entre le monde "réel" et le monde "perçu". Le monde perçu est inévitablement brouillé par l'imperfection de nos sens. La physique nous apprend qu'il existe aussi un brouillage "objectif", reflétant la nature physique du monde indépendamment de nos sens. Au niveau microscopique (quantique), le principe d'incertitude d'Heisenberg implique qu'une particule, comme un électron, n'a de "réalité" que si l'on effectue une mesure sur elle, et cette mesure modifie ses propriétés. Au niveau macroscopique, les "mirages gravitationnels" déforment notre vision de l'Univers. Ceux-ci résultent de la courbure de l'espace-temps. Les rayons lumineux émis par les astres lointains (galaxies, quasars) rencontrent sur leur trajet jusqu'à nous des masses (étoiles, galaxies, amas de galaxies); en courbant l'espace dans leur voisinage, ces masses intermédiaires perturbent les trajets des rayons lumineux et engendrent des illusions d'optiques, des "mirages" qui déforment, amplifient ou démultiplient les images des sources situées à l'arrière-plan.
Avec les modèles d'Univers chiffonnés, le brouillage cosmique pourrait être complet, et non plus localisé dans certaines directions d'observation. Là, ce serait la forme globale de l'espace qui démultiplierait les trajets de la lumière entre les sources lointaines et nous, de sorte que nous serions plongés dans un univers d'apparence très différente de ce qu'il est en réalité. Par exemple, chaque galaxie "réelle" aurait des dizaines d'images fantômes réparties dans toutes les directions du ciel, mais qu'il serait difficile de reconnaître en tant que telles. L'univers nous paraîtrait vaste, "déplié", contenant des milliards de galaxies, tandis qu'il serait en réalité beaucoup plus petit, chiffonné, contenant beaucoup moins d'objets qu'on n'en voit. Ce miroir-aux-alouettes cosmique plongerait le cosmologiste entre l'illusion de l'infini et une réalité finie.

|
L'illusion cosmique
On peut envisager l'espace comme un jeu de Pac Man, où les personnages
qui sortent par un bord de l'écran réapparaissent sur le bord
opposé. Cette configuration est celle d'un tore, puisqu'on obtient un
tore en recollant les bords opposés d'un carré. On peut reprendre
cette idée de recollement à trois dimensions : si l'Univers
était comme l'intérieur d'une boîte dont les faces
opposées étaient recollées, le nombre de galaxies nous
paraîtrait bien supérieur à ce qu'il est en
réalité. Sur cette figure, on a représenté les
résultats d'une simulation où l'on a placé au hasard un
vingtaine de galaxies dans un modèle d'Univers "hypertorique" dont la
taille est d'un milliard d'années-lumière seulement (a). L'aspect
du ciel ne se réduit pas aux images des vingt galaxies (b), car les
rayons lumineux empruntent de multiples trajets pour nous parvenir. Au
contraire, l'image de chacune des "vraies" galaxies est
démultipliée en un grand nombre d'images "fantômes", qui
donnent à l'Univers l'apparence d'être beaucoup plus vaste et
peuplé (c).
|
La quatrième étape clé de la cosmologie est à venir. Elle résidera peut-être dans la résolution des problèmes de l'infini, non seulement liés à l'espace et au temps, mais également à ceux présents dans les singularités.
Dans les modèles de big bang, la singularité initiale est un état de dimension nulle, de courbure et de densité infinies, qui surgit inévitablement quand on remonte à l'envers l'histoire de l'expansion cosmique. A la singularité, les lois de la physique deviennent incohérentes et perdent tout pouvoir prédictif. Cette singularité ne peut être évitée par les lois classiques (non quantiques).
L'Univers quantique
Peut-on légitimement remonter le passé cosmique jusqu'à la singularité ? Non : lorsque les dimensions de la "bulle" d'univers observable (aujourd'hui 10^28 centimètres) étaient inférieures à 10^(-33) centimètre (correspondant, selon les modèles actuels, à un temps plus petit que 10^(-43) seconde), la relativité générale classique perd tout pouvoir prédictif car les effets quantiques deviennent prépondérants : une théorie de la gravitation quantique devient impérative, nécessitant une unification complète des quatre interactions physiques (électromagnétique, forte, faible, gravitationnelle).
Cependant cette théorie n'existe pas, en raison de difficultés fondamentales liées à la nécessaire redéfinition de concepts tels que l'espace, le temps, la causalité, le rôle de l'observateur, etc. De nombreuses propositions ont été faites : supercordes, introduction de dimensions supplémentaires, etc. Ce n'est pas le lieu de les recenser, mais je considérerai l'une des approches, celle de la cosmologie quantique.
La cosmologie quantique résulte de l'application des principes de la mécanique quantique à la description de l'Univers dans son ensemble. Elle tente de répondre de façon rationnelle aux questions des origines (d'où venons-nous ?) et de la contingence (pourquoi y a-t-il quelque chose plutôt que rien?). La description de la dynamique de l'Univers à l'échelle quantique a initialement été proposée dans les années 1960 par John Wheeler et Bryce de Witt : au niveau microscopique, la géométrie de l'univers devient "floue", comparable à une sorte d'écume constamment agitée de petites fluctuations. Les équations de Wheeler-de Witt permettent, en principe, de calculer les probabilités pour que l'univers ait telle ou telle configuration de l'espace et de la matière, mais, en pratique, les équations sont inutilisables sous leur forme générale, car bien trop complexes. La seule chance d'en trouver des solutions est de simplifier considérablement le problème. Ainsi, la cosmologie quantique ne peut être mise en oeuvre que pour des modèles très simples, ce qui réduit sa portée par rapport aux ambitions théoriques originelles. Divers solutions approchées ont été proposées, notamment par "l'école russe" (A. Lindé, A. Vilenkin) et par "l'école anglo-saxonne" (J. Hartle et S. Hawking). En termes simples, le modèle quantique de Hartle et Hawking n'a ni frontière ni bord, comme la surface d'une sphère mais avec deux dimensions supplémentaires. Autrement dit, l'Univers serait fini non seulement dans l'espace (son "volume" total serait fini) mais aussi dans le temps. La problématique singularité initiale disparaîtrait : l'Univers n'aurait pas eu de commencement et n'aurait jamais de fin. Cependant cette nouvelle "éternité du temps" ne serait trouvée qu'au prix de l'abandon du temps cosmique réel (mesuré par les horloges ou par l'expansion des galaxies) au profit d'un temps imaginaire (au sens mathématique du terme).
L'approche de A. Lindé, bien différente, suppose des conditions initiales chaotiques. Qualitativement, Lindé présente sa solution (non exacte) sous la forme d'un gigantesque univers éternel et auto-reproducteur, constitué d'une "mousse d'Univers". Chaque bulle de cette mousse aurait ses propres caractéristiques : constantes physiques, nombre de dimensions spatiales, dynamique. Notre Univers observable ne serait qu'une infime partie de l'une de ces bulles, démesurément gonflée par l'inflation. Là encore, l'Univers "global" n'aurait ni commencement ni fin, même si les bulles individuelles, avec notamment ce qui semble être "notre univers", pouvaient naître et mourir.
|
|
L'ÉCUME DE L'ESPACE-TEMPS La structure de l'Univers est envisagée différemment selon les modèles physiques sous-jacents. Ici on a représenté : - un modèle classique (non quantique), où l'espace est lisse à toutes les échelles, - un modèle où la structure à petite échelle est agitée de fluctuations quantiques, - un modèle où l'Univers n'est qu'une bulle au sein d'une mousse composée d'un nombre infini de bulles, chacune ayant ses propres lois physiques.
|
Si la cosmologie quantique éclaire les débuts de l'Univers, elle soulève de très nombreux problèmes. C'est d'ailleurs ce qui fait son intérêt. Résout-elle le problème de la singularité ? Oui dans certains modèles, non dans d'autres. Elle ne résout pas non plus le problème de la topologie de l'Univers.
Je conclurai ce panorama des quelques idées clefs des cosmologies anciennes, contemporaines et futures en laissant la parole au poète Omar Khayyâm (XIe-XIIe siècles) :
 A LIRE :
A LIRE :
J. BARROW : La grande théorie, Albin Michel, 1994
J. DEMARET : Univers, Le Mail, 1991
R. HAKIM : La science et l'univers, Syros, 1992
A. KOYRÉ : Du monde clos à l'univers infini, Le Livre de Poche, 1992
J.-P. LUMINET et M. LACHIÈZE-REY : La Physique et l'infini , Flammarion/Dominos, 1994
