


par Jean-Pierre Luminet
Directeur de Recherches au CNRS
Astrophysicien à l'Observatoire de Paris-Meudon.
La relativité générale bouleverse les concepts même de temps et d'espace. L'univers n'a pas une structure d'espace euclidien immuable tissé par un temps indépendant; c'est un espace-temps déformé par la présence de matière. Manifestation de la courbure de l'espace-temps, la gravitation dicte les trajectoires des particules matérielles et des rayons lumineux, astreints à épouser les contours d'une géométrie quadridimensionnelle non euclidienne.
Les équations fondamentales de la relativité décrivent la façon dont le contenu matériel de l'univers détermine la géométrie de l'espace-temps. De cette manière, la théorie permet de décrire l'univers dans son ensemble selon des modèles cosmologiques plausibles. Parmi les solutions que permet la théorie, certaines seulement décrivent correctement l'univers sans entrer en contradiction avec les observations astronomiques.
Einstein construisit en 1917 le premier modèle d'univers fondé sur sa théorie de la relativité. Sa grande trouvaille fut de proposer une approche nouvelle de la question de l'espace fini ou infini. En effet, la géométrie non-euclidienne permet de représenter précisément un espace à la fois fini et sans limite : l'hypersphère. Einstein offrit donc, pour la première fois dans l'histoire de la cosmologie, un modèle d'univers fini échappant à tout paradoxe de "bord".
Les partisans d'un monde fini ont longtemps buté sur une
difficulté fondamentale. Il semblait indispensable d'imaginer au
Monde
un centre et une frontière, mais Archytas de Tarente, pythagoricien
du
Ve siècle, énonca un paradoxe visant à
démontrer
l'absurdité de l'idée d'un bord matériel du monde. Son
argument connut une fortune considérable dans tous les
débats sur
l'espace : "Si je suis à l'extrémité du ciel,
puis-je
allonger la main ou un bâton ? Il est absurde de penser que je ne le
peux
pas; et si je le peux, ce qui se trouve au-delà est soit un corps,
soit
l'espace. Nous pouvons donc aller au-delà de cela encore, et ainsi
de
suite. Et s'il y a toujours un nouvel espace vers lequel on peut tendre le
bâton, cela implique clairement une extension sans limites".
Si ce qui est au delà du Monde fait toujours partie du Monde, le
Monde
ne peut logiquement être borné sans qu'il y ait paradoxe! Il
fallut attendre le développement des géométries non
euclidiennes au XIXe siècle pour résoudre la controverse. Ces
géométries permettent de concevoir des espaces finis sans
avoir
de bord (tout comme, à deux dimensions, la surface d'une
sphère)
et considérer sans paradoxe un univers fini. Cette conception n'est
pas
si naturelle et la confusion se retrouve encore aujourd'hui dans nombre
d'esprits; lorsque, par exemple, un conférencier décrit
l'expansion de l'univers, il se voit souvent poser la question : dans quoi
l'univers gonfle-t-il? La réponse est que l'univers ne gonfle dans
rien
du tout, puisqu'il n'y a pas d'espace en dehors de lui-même !
Mais
pour le comprendre vraiment, il faut adopter un cadre mental non
euclidien.
A côté de la révolution conceptuelle issue de la relativité, les progrès observationnels conduisirent Hubble à annoncer, en 1929, que les autres galaxies s'éloignent systématiquement de la nôtre, avec des vitesses proportionnelles à leur distance. Le modèle d'Einstein dut donc être abandonné car il décrivait un univers statique, au profit de modèles d'univers dynamiques explorés indépendamment par le russe Alexandre Friedmann et par le belge Georges Lemaître.
La question de la finitude ou de l'infinitude de l'espace est parfaitement bien posée dans le cadre des modèles de Friedmann-Lemaître, appelés plus communément "modèles de big bang". Ces modèles supposent que l'univers a partout les mêmes propriétés (l'espace est dit "homogène et isotrope"). Ces propriétés sont de deux sortes seulement : la courbure, constante dans l'espace mais dont il reste à préciser le signe, et la topologie. En ce qui concerne la courbure, trois familles d'espaces sont considérées : l'espace euclidien (c'est à dire à courbure nulle, celui dont nous connaissons bien les propriétés), l'espace sphérique (à courbure positive) et l'espace hyperbolique (à courbure négative). L'espace sphérique est, dans tous les cas, fini (c'est l'une des raisons pour lesquelles Einstein, fils de Parménide, le choisit initialement). Pour les espaces des deux autres familles, le caractère fini ou infini dépend de la topologie. Dans les versions les plus simples toutefois, ils sont infinis.
Les cosmologues négligent le plus souvent l'aspect "topologie" pour ne considérer que la courbure. Cette simplification est cruciale quant au problème de l'infini spatial puisque, dans ce cas, le dilemme fini/infini se ramène à connaître le signe de la courbure de l'espace.
La relativité générale indique comment calculer cette courbure. Sa valeur dépend de la densité moyenne de matière qu'il contient, ainsi que d'une constante Lambda appelée constante cosmologique. Le plus souvent, une seconde simplification est introduite, celle de supposer cette constante nulle. Alors, le caractère fini/infini ne dépend plus que de la densité moyenne de matière : selon qu'elle est supérieure ou inférieure à une certaine "valeur critique" de 10^(-29) g/cm^3, la courbure est positive ou négative, et l'espace fini ou infini.
Que montrent les observations ? Elles indiquent une densité moyenne environ dix fois inférieure à la valeur critique. Apparemment, si l'on néglige les complications topologiques et la constante cosmologique, l'espace serait donc infini. De fait, la valeur observée n'est qu'une limite inférieure. Il serait vain de croire que nous voyions toute la matière de l'univers. Différentes raisons suggèrent qu'existent en plus de grandes quantités de masse cachée, suffisamment peut-être pour que la densité réelle de l'univers atteigne la valeur critique. Dans ce cas, l'univers resterait marginalement ouvert dans l'espace et dans le temps. C'est le modèle euclidien qu'Einstein et de Sitter proposèrent en 1931, et qui garde encore aujourd'hui les faveurs de nombreux cosmologues sans que rien de déterminant ne le justifie (sinon ... un sentiment esthétique!)
|
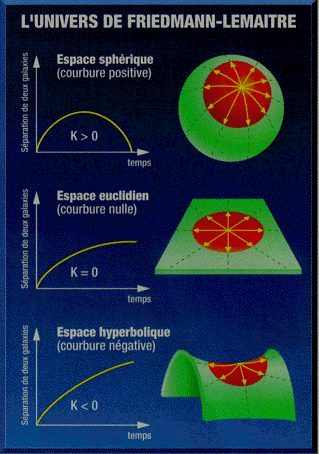
L'Univers est-il fermé ou ouvert?
Dans les modèles cosmologiques de Friedmann-Lemaître
à constante cosmologique nulle, la courbure est directement
liée
à la densité : courbure positive (espace sphérique)
lorsque la densité est supérieure à la valeur
critique,
courbure nulle (espace euclidien) si elle est égale à la
valeur
critique et courbure négative (epace hyperbolique) si elle est
inférieure. La courbure dicte donc seule l'évolution
temporelle :
l'univers est temporellement fermé dans le cas sphérique,
temporellement ouvert dans les cas euclidien et hyperbolique. Le
modèle
euclidien d'Einstein-de Sitter de 1931 (que certains estiment
favorisé
par le modèle de l'inflation) correspond au schéma du
milieu. Dans les modèles de Lemaître à constante cosmologique non nulle, la courbure est liée à la densité de matière et à la constante cosmologique. Il n'y a plus de lien direct entre la courbure et la dynamique temporelle de l'univers : celui-ci peut être sphérique mais temporellement ouvert. Si, en outre, la topologie n'est pas simple, il n'y a plus aucune correspondance entre finitude/infinitude temporelle et finitude/infinitude spatiale.
|
Si le paradoxe du bord a fait obstacle à l'espace fini, le
"paradoxe de
la nuit noire" a fait obstacle à l'infini cosmique.
L'obscurité
de la nuit cache en effet un mystère impliquant le cosmos tout
entier,
son extension et son histoire. Il s'énonce comme suit : si
l'espace
est infini et uniformément rempli d'astres, en quelque direction que
l'on regarde on doit finir par trouver une étoile sur la ligne de
visée. Autrement dit, le fond du ciel devrait être une
tapisserie
radieuse continûment composée d'étoiles, ne laissant
aucune
place au noir. Pourquoi n'en est-il pas ainsi ? La question, posée
dès le XVIIe siècle par Kepler, souleva des dizaines
d'explications et de modèles. C'est l'écrivain
américain
Edgar Poe qui fournit la première réponse satisfaisante.
Dans un
texte prémonitoire intitulé Eurêka, Poe expliqua que le
noir de la nuit reposait sur la finitude du temps cosmique. En effet,
la lumière ne se propage qu'à vitesse finie. Or, dans un
univers
temporellement fini, les étoiles n'ont pas toujours existé.
Nous
ne pouvons donc recevoir leur lumière que si celle-ci a eu le temps
de
nous atteindre, c'est à dire si les étoiles qui l'ont
émise sont suffisamment proches. Ainsi, le ciel n'est pas
uniformément brillant parce que les étoiles (pas
nécessairement l'univers tout entier) n'existent que depuis un temps
fini.
En comprenant comment l'obscurité nocturne était riche
d'enseignement sur la finitude temporelle du monde, Poe anticipait de
plusieurs
décennies sur les modèles relativistes du big-bang.
|
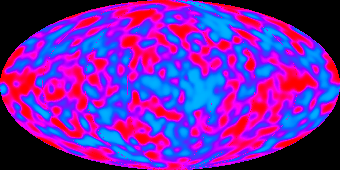
Le rayonnement du fond de ciel.
Puisque l'univers n'existe (sinon en tant qu'univers, du moins dans un
état permettant l'existence des étoiles) que depuis quelques
milliards d'années, le fond du ciel n'est guère brillant. Il
émet une faible lueur, imperceptible à nos yeux, mais que les
radiotélescopes ont captée en 1965; c'est le vestige de
l'éblouissant feu primitif refroidi par quinze milliards
d'années
de voyage.
|
Les questions relatives à la forme globale de l'espace et, en particulier, son extension finie ou infinie, relèvent en dernière analyse, non pas de la relativité générale (une théorie physique locale) mais de la topologie (théorie mathématique globale).
Rien n'oblige l'espace à posséder la topologie la plus simple (dite "simplement connexe") car la relativité générale n'impose aucune contrainte sur les propriétés globales de l'espace-temps. De nombreuses "variantes" topologiques d'espace à trois dimensions peuvent donc être utilisées pour construire des modèles d'univers pertinents, c'est-à-dire compatibles à la fois avec la relativité et avec les observations.
Grâce aux topologies "multi-connexes", il devient possible de considérer des modèles d'univers où l'espace est fini quelle que soit sa courbure, même si la densité de matière et la constante cosmologique sont très faibles.
Historiquement, c'est W. de Sitter qui fit remarquer en 1917 à Einstein que son modèle d'univers statique et sphérique pouvait s'accommoder d'une topologie différente, à savoir celle de l'espace projectif. La différence n'était pas très grande car ces deux variantes sont finies. C'est dans l'article fondateur de Friedmann, en 1922, qu'il est fait mention pour la première fois d'une variante topologique finie de l'espace euclidien (normalement infini). Ceci resta ignoré d'Einstein qui, en 1931, publia avec de Sitter un article où ils optaient pour le modèle euclidien infini. Ce n'est qu'en 1958 que Lemaître mentionna l'existence d'espaces hyperboliques compacts, eux aussi susceptibles d'être appliqués aux modèles de big bang. Malgré cela, le sujet est toujours resté confidentiel et largement ignoré de la communauté des chercheurs.
Outre l'intérêt de "compactifier" des espaces infinis, les modèles d'espace multi-connexe sont source de bien des surprises en créant une "illusion de l'infini". Voyons pourquoi. Pour construire des espaces multi-connexes, les mathématiques nous enseignent que l'on peut partir de l'un des trois types d'espaces "ordinaires" (simplement connexes). Ensuite, l'identification de certains points les uns aux autres fait changer la forme de l'espace et le rend multi-connexe. A partir de quoi l'on peut construire des modèles d'univers, où l'espace est fini (bien que la courbure puisse être négative ou nulle) et de volume réellement petit. On les appelle "mini-univers". L'exemple le plus simple est celui où notre espace serait un hypertore ayant un rayon inférieur à dix milliards d'années-lumière. Dans ce cas, les rayons lumineux auraient eu le temps de faire plusieurs fois le tour de l'univers. Cela impliquerait que chaque objet cosmique (chaque galaxie par exemple) devrait apparaître selon autant d'images fantômes, observables dans différentes régions du ciel. L'univers observé nous apparaîtrait donc constitué de la répétition d'un même ensemble de galaxies.
Il n'est pas facile de vérifier si nous vivons ou non dans un mini-univers. Les images fantômes de chaque galaxie "réelle" nous apparaîtraient dans des directions différentes, avec des éclats différents, sous des orientations différentes, et à des époques différentes de l'évolution de la galaxie en question. Il serait pratiquement impossible de les reconnaître comme telles! L'univers pourrait nous paraître vaste, "déplié", rempli de milliards de galaxies, tandis qu'il serait en réalité beaucoup plus petit, "replié" mais ne contenant qu'un petit nombre d'objets authentiques. Une énorme illusion d'optique cosmique! Bien sûr, les données observationnelles actuelles permettent d'éliminer la possibilité d'un univers trop petit... sinon nous aurions déjà reconnu, proches de nous, des images multiples de notre propre Galaxie! Divers arguments de ce genre, appliqués à quelques objets cosmiques (les amas de galaxies les plus proches), permettent d'exclure un univers dont les dimensions seraient inférieures à quelques centaines de millions d'années-lumière. Des études statistiques sur la distribution des amas de galaxies révéleront peut-être la nature "chiffonnée" de l'espace sur une échelle de quelques milliards d'années-lumière.

|
Nous voyons un ciel rempli de galaxies, mais son aspect ne permet
pas de
décider si les galaxies des régions lointaines sont ou non
des
images fantômes de galaxies plus proches. L'hypothèse d'un
Univers
multiconnexe ne peut être écartée : l'Univers pourrait
nous
paraître vaste, "déplié", tandis qu'il serait en
réalité beaucoup plus petit et "replié".
|
La topologie est la branche de la géométrie qui classifie
les
espaces en fonction de leur forme globale. Par définition, les
espaces
d'une même classe peuvent se déduire les uns des autres par
déformation continue, sans découpage ni déchirure.
Dans le
cas des espaces à deux dimensions, c'est à dire des
surfaces, la
sphère, par exemple, a la même topologie que n'importe quelle
surface fermée ovoïde. Mais le plan est de topologie
différente, puisqu'aucune déformation continue ne lui
donnera la
forme d'une sphère.
Pour mieux visualiser ce qu'est la topologie, partons du plan euclidien
ordinaire. C'est un feuillet infini à 2 dimensions (que l'on
imagine le
plus souvent dans l'espace à 3 dimensions). Découpons une
bande
de "longueur" infinie mais de largeur finie; puis identifions (recollons)
les
deux bords de cette bande : on obtient un cylindre, c'est à
dire
une surface de topologie différente de celle du plan initial.
Prenons
une autre feuille infinie et, cette fois, découpons-la en rectangle.
Identifions deux à deux les bords parallèles. Nous obtenons
une
surface fermée, finie. C'est un tore. A partir d'une simple feuille
de
papier nous avons donc défini 3 surfaces de topologies
différentes, appartenant à la même famille de courbure
nulle : les surfaces localement euclidiennes (ce ne sont pas les seules).
Les mathématiciens se sont attachés à la
classification
des espaces à trois dimensions. Comme les surfaces, les espaces
peuvent
d'abord être rangés, selon le signe de leur courbure, en type
sphérique, type euclidien ou type hyperbolique. Ensuite on
dénombre les variantes topologiques à l'intérieur de
chacune de ces familles. Il existe par exemple 18 sortes d'espaces
tridimensionnels à courbure nulle, de topologies distinctes. Le plus
simple est l'espace euclidien "ordinaire", celui dont on apprend les
propriétés sur les bancs des écoles, mais d'autres
sont
fermés et finis. C'est par exemple le cas de l'hypertore, qui
généralise à trois dimensions le cas du tore. Un
hypertore
peut être considéré comme l'intérieur d'un cube
ordinaire, dont les faces opposées deux à deux sont
identifiées : en sortant par l'une, on rentre
immédiatement
par celle qui est opposée. Un tel espace est fini.
D'autre part, il y a une infinité de formes d'espaces à
courbure
positive, toutes finies, et une infinité d'espaces à
courburenégative, certaines fermées (finies) et les autres
ouvertes (infinies).
Pour les visualiser, on les représente par l'intérieur d'un
polyèdre dont certaines faces sont identifiées deux à
deux.
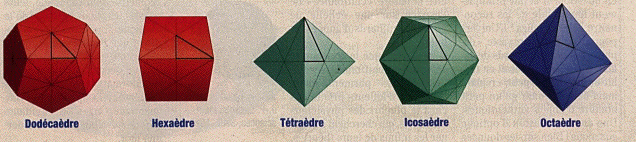
Les cinq polyèdres réguliers, déjà invoqués par Platon pour géométriser les "éléments" Terre, Eau, Air, Feu, Quintessence, servent aujourd'hui à représenter certains espaces multi-connexes, à condition de considérer que les faces sont indentifiées par paires selon certaines transformations géométriques.
|
|
Un espace hyperbolique compact. L'intérieur d'un dodécaèdre régulier, dont les faces pentagonales sont identifiées ("collées") par paires, est un espace fermé de courbure négative. Vu de l'intérieur, on aurait l'impression de vivre dans un espace cellulaire, pavé à l'infini par des dodécaèdres déformés par des illusions d'optique. Copyright 1990 by The Geometry Center, University of Minnesota.
|
Qui n'a pas été fasciné par les jeux de miroirs? Qu'il s'agisse de la Galerie des Glaces du Château de Versailles ou des plus modestes Palais des Glaces des attractions foraines, chacun s'émerveille de l'illusion engendrée par les images fantômes. Les miroirs recèlent certains secrets de l'infini.
Tout le monde a constaté que tapisser de miroirs les murs d'une pièce donne l'illusion d'une pièce plus grande.
Prenons une pièce tapissée de miroirs sur ses six parois (plancher et plafond compris). Si vous pénétrez dans la pièce, par le jeu des multiples réflexions sur les parois vous avez immédiatement l'impression de voir l'infini, comme si vous étiez suspendu au sommet d'un puits sans fond, prêt à être avalé dans une direction ou une autre au moindre mouvement.
Il pourrait bien en être ainsi de l'espace cosmique!
|
|
Il se peut que la topologie de l'univers soit multiconnexe,
c'est-à-dire que l'espace ressemble à l'intérieur
d'une
pièce tapissée de miroirs compliqués. Cette
multiconnexité créerait dans l'univers des chemins
supplémentaires pour les rayons lumineux qui nous parviennent des
galaxies lointaines. Il en résulterait un grand nombre d'images
fantômes de ces galaxies. Les schémas sont issus de
récentes simulations numériques d'univers
"chiffonnés",
effectuées avec mes collaborateurs. schéma du haut : l'espace est un hypertore, représenté par l'intérieur d'une cube de 5 milliards d'années-lumièe de côté dont les faces opposées sont identiques. 50 galaxies sont distribuées au hasard dans l'espace. schéma du milieu : positions, sur un planisphère céleste, des 50 galaxies "originales".
schéma du bas : apparence du ciel tenant compte des multiples
trajets
des rayons lumineux. Chaque galaxie "réelle" engendre une
cinquantaine
d'images "fantômes". Il est impossible de reconnaître les
images
"réelles" des images fantômes. Si l'on note la ressemblance
de ce
schéma avec l'apparence du vrai ciel, on en déduit qu'il est
tout
à fait possible que nous vivions dans une illusion d'optique
cosmique
nous donnant l'impression, non pas de l'infini, mais de l'immense, alors
que
l'espace réel serait petit et "chiffonné".
|
Il est clair que le concept de petit univers chiffonné relève de l'esthétique parménidienne. Celle-ci a d'ailleurs pris le pas chez la plupart des physiciens modernes, qui cherchent à éliminer les infinis de leurs théories. L'infinitude spatiale n'est pas le seul infini de la cosmologie relativiste. La théorie prédit en effet des configurations où certaines quantités géométriques (la courbure) et physiques (densité d'énergie, température) deviennent infinies : les singularités gravitationnelles. Les plus connues sont la singularité initiale du big bang, et la singularité terminale cachée au fond d'un trou noir. Les physiciens doutent qu'une théorie accouchant de singularités puisse être correcte. Le fait est que la relativité générale est incomplète, puisqu'elle ne tient pas compte des principes de la mécanique quantique. Cette dernière gouverne l'évolution du monde microscopique, en particulier le domaine des particules élémentaires. Sa caractéristique essentielle est de donner une description "floue" des phénomènes, dans la mesure où les événements ne peuvent être calculés qu'en termes de probabilités. Or, le phénomène des singularités met en jeu la structure de l'espace-temps à très petite échelle. Il existe une longueur (appelée longueur de Planck, égale à 10^(-33) centimètre) représentant la plus petite dimension à laquelle l'espace-temps peut encore être considéré comme lisse. En-dessous, la texture même de l'espace-temps ne serait plus continue mais, tout comme la matière et l'énergie, formée de petits grains. Les infinis gravitationnels seraient remplacés par des fluctuations quantiques de l'espace-temps.
Avec la "cosmologie quantique", théorie à peine ébauchée et promise à de fascinants développements, se profilent des univers multiples, simultanés, sans interaction entre eux, ne différant les uns des autres que par leur géométrie, leur topologie, leurs constantes fondamentales de la physique.
Tous ces univers ne seraient que l'écume de l'Univers majuscule, lui infini et éternel, sorte d'océan bouillonnant, en transformation perpétuelle, que les physiciens appellent le "vide quantique". On le voit, les enfants d'Héraclite n'ont pas dit leur dernier mot...
|
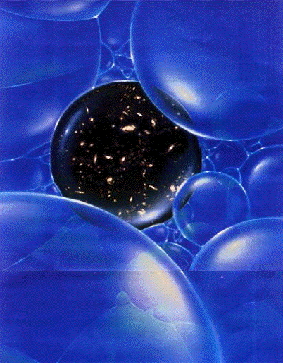
L'écume du Vide La cosmologie quantique permet d'envisager des univers multiples, sans interaction entre eux. Notre univers observable occuperait une "bulle" transitoire, située au sein d'une "écume" formée par toutes les bulles nées des fluctuations spontanées du vide quantique.
Copyright : Manchu/Ciel et Espace
|
Créature hybride enfantée par la géométrie
non-euclidienne et la gravitation relativiste, le trou noir offre deux
jolis
problèmes d'infini : un faux et un vrai. Un trou noir
résulte de
l'effondrement gravitationnel d'une masse en dessous d'un certain volume
critique. Comme le bord d'un puits sans fond creusé dans la trame
élastique de l'espace-temps, sa surface marque la frontière
géométrique d'une zone de non-retour. Pour un observateur
extérieur, les battements d'une horloge placée près du
trou noir se ralentissent au fur et à mesure que l'horloge est plus
proche de la surface, jusqu'à se figer lorsque l'horloge atteint la
surface. Tout se passe alors comme si le temps était
indéfiniment
gelé. En conséquence, le trou noir lui-même est
inobservable, car rejeté à l'infini dans le futur de tout
observateur. Cet infini n'est qu'apparent car il peut être
résorbé dans une représentation correcte (en temps
propre)
des phénomènes.
Il en va tout autrement avec l'intérieur du trou noir. La
théorie prédit l'existence d'un infini inéluctable
à l'intérieur du trou noir : une singularité,
où la
courbure et la densité de matière deviennent infinies.
Un voyageur explorant les environs d'un trou noir serait plongé dans des illusions d'optique. Trompé par le faux infini lié à la surface du trou, il ne verrait jamais l'intérieur, à moins d'y plonger en personne et de découvrir à ses dépens le vrai infini de la singularité!