Relativité d'échelle
et espace-temps fractal
 La théorie
de la relativité d'échelle se donne pour but d'étudier
les conséquences de l'abandon de l'hypothèse de différentiabilité
du continuum espace-temps (autrement dit, ce qui se passe quand on ne peut
plus définir de pente pour les coordonnées: voir figures).
Trois conséquences, au minimum, apparaissent du fait de cette généralisation:
La théorie
de la relativité d'échelle se donne pour but d'étudier
les conséquences de l'abandon de l'hypothèse de différentiabilité
du continuum espace-temps (autrement dit, ce qui se passe quand on ne peut
plus définir de pente pour les coordonnées: voir figures).
Trois conséquences, au minimum, apparaissent du fait de cette généralisation:
 (i) L'espace-temps
devient fractal, au sens où sa description géométrique
nécessite de faire intervenir explicitement l'échelle de
résolution à laquelle on le considère.
(i) L'espace-temps
devient fractal, au sens où sa description géométrique
nécessite de faire intervenir explicitement l'échelle de
résolution à laquelle on le considère.
(ii) Il existe une infinité de trajectoires possibles (indéterminisme)
quand une seule était attendue classiquement (déterminisme).
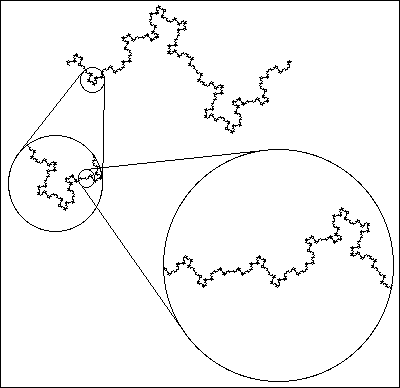
Ces trajectoires sont définies comme les géodésiques
(les lignes "les plus courtes") de l'espace-temps, et sont par conséquent
elles-mêmes fractales. (Voir ci-contre des exemples d'une telle courbe,
qui montre des structures à toutes les échelles ou au moins
sur une large gamme d'échelles différentes).
(iii) Il y a irréversibilité sous l'inversion du temps
au niveau infinitésimal (réflexion sur l'intervalle dt <-->
-dt).
Ces trois effets sont alors combinés pour construire un opérateur
de dérivation "covariante" par rapport au temps. Celui-ci décrit
les effets induits par les structures fractales (en échelle) sur
les déplacements dans l'espace. L'équation fondamentale de
la dynamique newtonienne, écrite à l'aide de cet opérateur,
s'intègre alors sous forme d'une équation de Schrödinger
(l'équation fondamentale de la mécanique quantique non relativiste).
Ses solutions permettent de calculer des distributions de probabilité,
qu'on peut interpréter comme tendance du système à
former des structures.
Application à la gravitation:
exemple des systèmes planétaires
 La théorie
de la relativité d'échelle permet de poser d'une manière
nouvelle le problème de la formation et de l'évolution des
structures gravitationnelles. Par exemple, alors que, dans la théorie
standard, aucune structure ne peut se former à partir d'un milieu
de densité strictement constante (des fluctuations "initiales" sont
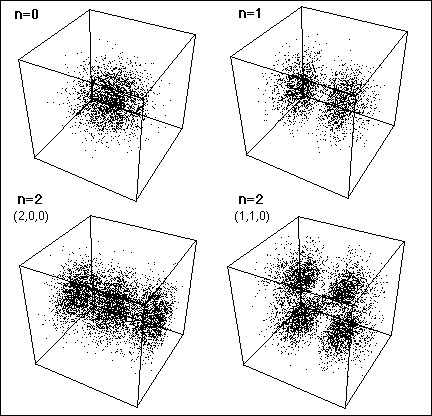
nécessaires), des structures se forment naturellement dans la nouvelle
approche, aux morphologies bien précises données par les
divers modes quantifiés d'un oscillateur harmonique tridimensionnel
isotrope (voir figure de gauche).
La théorie
de la relativité d'échelle permet de poser d'une manière
nouvelle le problème de la formation et de l'évolution des
structures gravitationnelles. Par exemple, alors que, dans la théorie
standard, aucune structure ne peut se former à partir d'un milieu
de densité strictement constante (des fluctuations "initiales" sont
nécessaires), des structures se forment naturellement dans la nouvelle
approche, aux morphologies bien précises données par les
divers modes quantifiés d'un oscillateur harmonique tridimensionnel
isotrope (voir figure de gauche).
 L'application aux
systèmes planétaires consiste à traiter le même
problème, mais maintenant dans le potentiel central képlerien
d'une étoile. Comme dans le modèle standard de formation,
les planètes sont supposées être formées par
accrétion de planétésimaux. Cependant, les mouvements
de ces petits corps dans la nébuleuse primitive sont tellement chaotiques
qu'au delà d'une certaine échelle de temps (dépendant
du système considéré), l'information sur les orbites
individuelles se perd. On admet que les trois conditions ci-dessus sont
alors réalisées, si bien que la distribution initiale de
densité de probabilité de ces planétésimaux
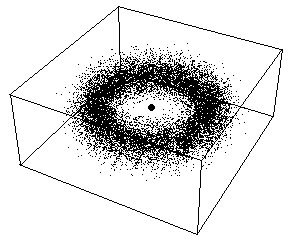
sera donnée par les solutions d'une équation de Schrödinger
gravitationnelle (figure de droite). Les positions finales des planètes
après accrétion se répartiront donc autour des pics
de probabilité prévus par ces solutions.
L'application aux
systèmes planétaires consiste à traiter le même
problème, mais maintenant dans le potentiel central képlerien
d'une étoile. Comme dans le modèle standard de formation,
les planètes sont supposées être formées par
accrétion de planétésimaux. Cependant, les mouvements
de ces petits corps dans la nébuleuse primitive sont tellement chaotiques
qu'au delà d'une certaine échelle de temps (dépendant
du système considéré), l'information sur les orbites
individuelles se perd. On admet que les trois conditions ci-dessus sont
alors réalisées, si bien que la distribution initiale de
densité de probabilité de ces planétésimaux
sera donnée par les solutions d'une équation de Schrödinger
gravitationnelle (figure de droite). Les positions finales des planètes
après accrétion se répartiront donc autour des pics
de probabilité prévus par ces solutions.
Retour à la Prédiction des orbites
Quelques publications sur le sujet:
L. Nottale, Fractal Space-Time and Microphysics (World Scientific, 1993,
333 pp.)
L. Nottale, 1996, Astron. Astrophys. Lett. 315, L9: "Scale
relativity and quantization of extra-solar planetary systems"
L. Nottale, 1996, Chaos, Solitons & Fractals, 7, 877:
"Scale relativity and Fractal Space-Time: Applications to Quantum Physics,
Cosmology and Chaotic Systems".
L. Nottale, G. Schumacher & J. Gay, 1997, Astron. Astrophys.
322,
1018: "Scale relativity and quantization of the Solar System".
L. Nottale, 1997, Astron. Astrophys. Lett.
327, 867: "Scale relativity and quantization of the Universe.
I. Theoretical framework".
R. Hermann, G. Schumacher G., R. Guyard, 1998, Astron. Astrophys.,
335,
281 "Scale relativity and quantization of the Solar System. Orbit quantization
of the planet's satellites".
L. Nottale, 1998, "La relativité dans tous ses états:
au-delà de l'espace-temps" (Hachette)
Pour plus d'informations, voir le site: relativité
d'échelle et espace-temps fractal
 La théorie
de la relativité d'échelle se donne pour but d'étudier
les conséquences de l'abandon de l'hypothèse de différentiabilité
du continuum espace-temps (autrement dit, ce qui se passe quand on ne peut
plus définir de pente pour les coordonnées: voir figures).
Trois conséquences, au minimum, apparaissent du fait de cette généralisation:
La théorie
de la relativité d'échelle se donne pour but d'étudier
les conséquences de l'abandon de l'hypothèse de différentiabilité
du continuum espace-temps (autrement dit, ce qui se passe quand on ne peut
plus définir de pente pour les coordonnées: voir figures).
Trois conséquences, au minimum, apparaissent du fait de cette généralisation:
 (i) L'espace-temps
devient fractal, au sens où sa description géométrique
nécessite de faire intervenir explicitement l'échelle de
résolution à laquelle on le considère.
(i) L'espace-temps
devient fractal, au sens où sa description géométrique
nécessite de faire intervenir explicitement l'échelle de
résolution à laquelle on le considère.
 La théorie
de la relativité d'échelle permet de poser d'une manière
nouvelle le problème de la formation et de l'évolution des
structures gravitationnelles. Par exemple, alors que, dans la théorie
standard, aucune structure ne peut se former à partir d'un milieu
de densité strictement constante (des fluctuations "initiales" sont
nécessaires), des structures se forment naturellement dans la nouvelle
approche, aux morphologies bien précises données par les
divers modes quantifiés d'un oscillateur harmonique tridimensionnel
isotrope (voir figure de gauche).
La théorie
de la relativité d'échelle permet de poser d'une manière
nouvelle le problème de la formation et de l'évolution des
structures gravitationnelles. Par exemple, alors que, dans la théorie
standard, aucune structure ne peut se former à partir d'un milieu
de densité strictement constante (des fluctuations "initiales" sont
nécessaires), des structures se forment naturellement dans la nouvelle
approche, aux morphologies bien précises données par les
divers modes quantifiés d'un oscillateur harmonique tridimensionnel
isotrope (voir figure de gauche).
 L'application aux
systèmes planétaires consiste à traiter le même
problème, mais maintenant dans le potentiel central képlerien
d'une étoile. Comme dans le modèle standard de formation,
les planètes sont supposées être formées par
accrétion de planétésimaux. Cependant, les mouvements
de ces petits corps dans la nébuleuse primitive sont tellement chaotiques
qu'au delà d'une certaine échelle de temps (dépendant
du système considéré), l'information sur les orbites
individuelles se perd. On admet que les trois conditions ci-dessus sont
alors réalisées, si bien que la distribution initiale de
densité de probabilité de ces planétésimaux
sera donnée par les solutions d'une équation de Schrödinger
gravitationnelle (figure de droite). Les positions finales des planètes
après accrétion se répartiront donc autour des pics
de probabilité prévus par ces solutions.
L'application aux
systèmes planétaires consiste à traiter le même
problème, mais maintenant dans le potentiel central képlerien
d'une étoile. Comme dans le modèle standard de formation,
les planètes sont supposées être formées par
accrétion de planétésimaux. Cependant, les mouvements
de ces petits corps dans la nébuleuse primitive sont tellement chaotiques
qu'au delà d'une certaine échelle de temps (dépendant
du système considéré), l'information sur les orbites
individuelles se perd. On admet que les trois conditions ci-dessus sont
alors réalisées, si bien que la distribution initiale de
densité de probabilité de ces planétésimaux
sera donnée par les solutions d'une équation de Schrödinger
gravitationnelle (figure de droite). Les positions finales des planètes
après accrétion se répartiront donc autour des pics
de probabilité prévus par ces solutions.