 La théorie
de la relativité d'échelle conduit à représenter
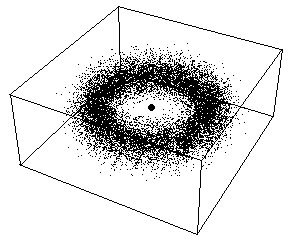
les orbites comme des lignes fractales à très petite échelle
(voir la rubrique pour en savoir plus ci-dessous);
il existe alors une infinité de trajectoires possibles, et une équation
statistique en régit les probabilités. Ces probabilités
ne sont pas uniformes, et on peut prédire comment vont se répartir
les planètes autour d'une étoile donnée, en fonction
de sa masse. Laurent Nottale et ses collaborateurs ont en particulier calculé
des prédictions sur les demi-grands axes et les excentricités
des orbites.
La théorie
de la relativité d'échelle conduit à représenter
les orbites comme des lignes fractales à très petite échelle
(voir la rubrique pour en savoir plus ci-dessous);
il existe alors une infinité de trajectoires possibles, et une équation
statistique en régit les probabilités. Ces probabilités
ne sont pas uniformes, et on peut prédire comment vont se répartir
les planètes autour d'une étoile donnée, en fonction
de sa masse. Laurent Nottale et ses collaborateurs ont en particulier calculé
des prédictions sur les demi-grands axes et les excentricités
des orbites.
vn = w0 / n
où n est entier et où w0 est une vitesse fondamentale et universelle. Des observations indépendantes aux échelles extragalactiques ont montré que cette constante était de l'ordre de 144 km/s. Le rapport ag = w0/c joue en fait le rôle d'une constante de couplage gravitationnelle.
En raison de la troisième loi de Kepler, v varie comme (M/a)1/2 ou encore comme (M/P)1/3, où M est la masse de l'étoile, a le demi-grand axe de l'orbite planétaire et P sa période. On prévoit donc des pics de probabilité pour des valeurs discrètes entières de la quantité 4.83(P/M)1/3 = 4.83(a/M)1/2. La constante 4.83 est la valeur de la vitesse fondamentale (144 km/s) en unités de vitesse de la Terre; la période (qui est la grandeur directement observée en ce qui concerne les nouvelles exoplanètes, à travers le mouvement de l'étoile qu'elles induisent) est en années; le demi-grand axe (a) est en unité astronomique (1 UA= 149.7 millions de kilomètres, définie par la distance Terre-Soleil); enfin la masse de l'étoile (M) est en unité de masse solaire.
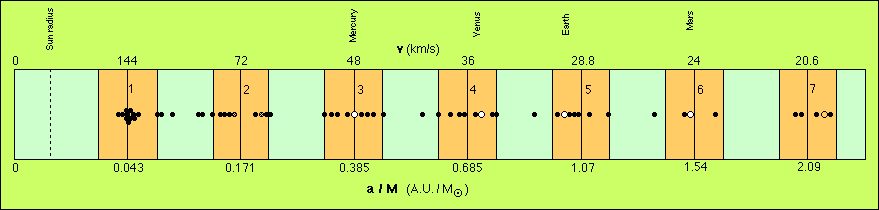
Les valeurs observées pour les exoplanètes découvertes depuis cinq ans (voir figures 1 et 2) sont en excellent accord avec ces prédictions: par exemple on trouve pour les deux premiers pics de probabilité a/M= 0.0438 +/- 0.0017 UA/Msol et 0.168 +/- 0.014 UA/Msol, à comparer aux valeurs prédites 0.0430 et 0.171 UA/Msol. Il en est de même pour le système de trois planètes découvertes autour du pulsar B1257+12, pour lesquelles l'accord relatif entre théorie et observations est de quelques dix-millièmes.

Figure 1. Distribution observée des demi-grands axes
(a) des orbites des exoplanètes et planètes du système
solaire interne (en unité naturelle de longueur pour ces systèmes,
donnée par la masse M de l'étoile). Les valeurs numériques
reportées sont celles de a/M et de la vitesse moyenne v (reliés
via la troisième loi de Kepler); l'échelle du tracé
est en racine de (a/M). On a porté en jaune les zones prévues
théoriquement pour être de haute probabilité et en
bleu celles de basse probabilité.
Rappelons que l'existence de ces pics (donc la possibilité de grande proximité entre les exoplanètes et leur étoile, qui a étonné au moment de leur découverte) a été prévue théoriquement (L. Nottale, 1993, Fractal Space-Time and Microphysics, World Scientific) avant cette découverte, qui remonte à 1995 en ce qui concerne les étoiles de type solaire.
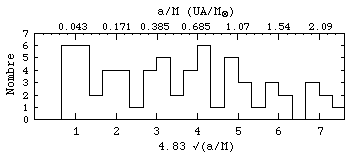
Figure 2. Histogramme de la distribution des demi-grands axes (ramenés à la masse de leur étoile), pour les planètes extrasolaires et les planètes du système solaire interne. Les masses des étoiles utilisées pour construire cet histogramme sont celles données par les auteurs de la découverte des exoplanètes (incertitudes de l'ordre de 10%, qui devient donc 3% pour (P/M)1/3). La distribution observée est non uniforme: des pics de densité de probabilité apparaissent de manière très précise aux positions prédites, sans aucun ajustement. La probabilité d'obtenir un tel résultat par hasard est inférieure à 2 10-5.
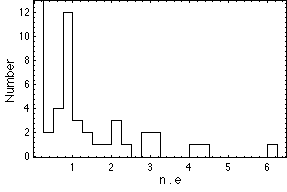
Figure 3. Histogramme de la distribution des excentricités (multipliées par le "nombre quantique" principal), pour les planètes extrasolaires et les planètes du système solaire interne. On prévoit des pics pour les valeurs entières de ce produit, ce que confirment les données d'observation. La probabilité d'obtenir un tel résultat par hasard est inférieure à 10-4. La probabilité combinée pour les deux effets de structuration (demi-grands axes et excentricités) est de 3 10-7.
Ces résultats vont dans le sens d'une universalité de
structure des différents systèmes planétaires, incluant
notre propre système solaire.
Références:
L. Nottale, G. Schumacher & E.T. Lefèvre, 2000, Astron. Astrophys. 361, 379: "Scale relativity and quantization of exoplanet orbital semi-major axes"
L. Nottale, N. Tran Minh, 2001, Astron. Astrophys. (soumis pour publication): "Scale relativity and quantization of exoplanet eccentricities"
Contact: L. Nottale (DAEC, Observatoire de Paris), N. Tran Minh (DAMAP, Observatoire de Paris)