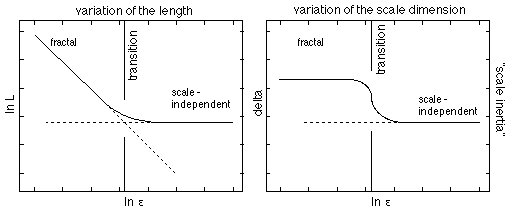
Figure 1. Loi d'échelle linéaire: comportement fractal auto-similaire de dimension fractale constante (avec transition vers une indépendance d'échelle macroscopique).
Applications de la relativité d'échelle aux sciences de la vie.
(Résumé).
L. NOTTALE
CNRS UMR 8102, LUTH, Observatoire de Paris-Meudon,
F-92195 Meudon Cedex, France
Lois d'échelle log-périodiques
Structure fractale de l'arbre de la vie
Log-périodicité dans les sociétés
Embryogenèse et développement humain
La théorie de la relativité d'échelle [1-8,18]
se donne pour but de décrire un espace-temps non-différentiable
ainsi que les multiples effets impliqués par une telle géométrie
nouvelle. Nous allons dans ce court résumé rappeler les étapes
de sa construction et introduire brièvement les applications possibles
de chacune de ces étapes aux sciences de la vie (paragraphes en
caractères gras).
1) Géométrie non-différentiable
et fractale
On démontre qu'un espace continu mais non-différentiable
est fractal, au sens où les longueurs dans un tel espace dépendent
explicitement de la résolution (i.e. de l'échelle d'observation)
et tendent vers l'infini quand l'échelle tend vers zéro.
2) Espace des échelles
On introduit alors un espace des échelles, qui est l'espace des
résolutions et de leurs transformations (c'est-à-dire des
"zooms", i.e. des transformation entre échelles).
3) Equations différentielles d'échelle
Les "objets" d'un tel espace sont donc structurés en échelle.
Ces structures sont considérées comme solutions d'équations
différentielles agissant dans cet espace des échelles. Autrement
dit, on décrit comment changent ces structures dans une transformation
d'échelle infinitésimale (un "zoom" infinitésimal).
4) Principe de relativité d'échelle
Ces équations différentielles sont contraintes par le principe de relativité d'échelle. Celui-ci se fonde sur l'interprétation des échelles d'observation comme caractérisant l'état d'échelle du système de coordonnées, et sur leur relativité (on ne peut définir que des rapports d'échelle, jamais des échelles absolues). Le principe de relativité d'échelle postule que les lois fondamentales de la nature doivent être valides quel que soit l'état d'échelle du système de référence. Il complète le principe de relativité de Galilée, Poincaré et Einstein, qui s'appliquait aux états de position, d'orientation et de mouvement.
5) Lois d'échelle
Des lois d'échelle de complexité croissante peuvent alors
être construites par la prise en compte de niveaux de complexité
croissants pour ces équations différentielles d'échelle.
5.1 Du linéaire au non-linéaire,
c'est-à-dire du premier au deuxième ordre de dérivation
en fonction des variables d'échelle, ou encore de l"inertie d'échelle"
à la "dynamique d'échelle".

Figure 1. Loi d'échelle linéaire: comportement
fractal auto-similaire de dimension fractale constante (avec transition
vers une indépendance d'échelle macroscopique).
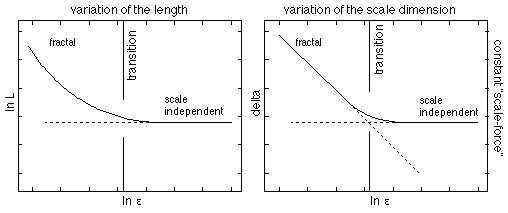
Figure 2. Loi d'échelle non-linéaire: dynamique
d'échelle avec force constante.
*CONFINEMENT:
Comportement à trois niveaux [14,15,18] (potentiel d'échelle
donné par un oscillateur harmonique): auto-similaire aux petites
échelles, indépendant d'échelle aux grandes échelles,
avec écart à l'invariance d'échelle dans une gamme
d'échelle intermédiaire (Fig.3). Appliqué
dans l'espace des échelles (i.e. à une variable déchelle
représentant une résolution), une telle solution décrit
un processus de confinement, par exemple un système compressé
qui "protège" ses petites échelles de la distorsion interne
due à sa contraction globale (seules les relativement grandes échelles
sont affectées par la distorsion, alors qu'on garde le comportement
auto-similaire aux petites échelles). Appliquée à
une variable r définissant une distance à
partir d'un centre, la variation de la dimension fractale représentée
Fig.3
(à droite) décrit un système à trois niveaux,
intérieur, extérieur et intermédiaire, la dimension
fractale prenant de très grandes valeurs dans la zone intermédiaire
(ce qui correspond à un "épaississement" des trajectoires).
On peut interpréter cette zone intermédiaire comme l'existence
d'une "peau" ou "membrane" séparant les domaines intérieur
et extérieur, ce qui est une des propriétés essentielles
des systèmes complexes (en particulier vivants).
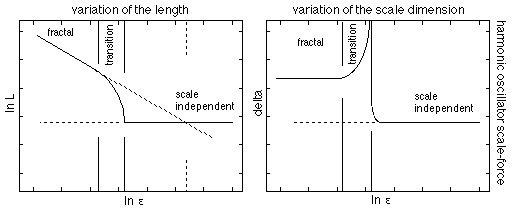
Figure 3. Loi d'échelle non-linéaire: dynamique
d'échelle avec potentiel d'oscillateur harmonique dans l'espace
des échelles.
*LOIS LOG-PERIODIQUES:
Comportement auto-similaire avec corrections log-périodiques
[9,14,15,18] (Fig.4).
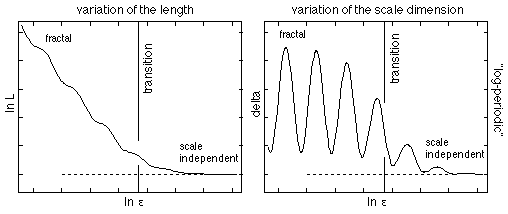
Figure 4. Loi d'échelle non-linéaire: corrections
log-périodiques à l'auto-similarité.
Ces structures montrent une invariance d'échelle discrète. On les obtient comme solutions d'une équation "d'onde d'échelle" du deuxième ordre [9]. Elles sont apparues aussi dès 1975 dans l'étude des phénomènes critiques comme solutions des équations du groupe de renormalisation (Nauenberg, Jona-Lasinio). De nombreux exemples de systèmes biologiques (hiérarchiques, arborescents) peuvent être décrits par cette approche (cf D. Sornette, 1998, Phys. Rep. 297, 239).
Figure 5a. Chronologie de lignées évolutives montrant
un comportement log-périodique.
Un modèle de structure fractale log-périodique pour plusieurs lignées évolutives de l'arbre de la vie a été proposé [10,11,13,14,17] (Fig. 5a).Cette description se caractérise par une accélération de la chronologie évolutive vers une époque critique spécifique à chaque lignée. Certaines lignées ont montré une décélération depuis leur époque d'apparition.
Figure 5b. Chronologie du rythme crise / non-crise dans les sociétés occidentales montrant une accélération log-périodique vers l'époque Tc=2080 +/- 30 [11,13].
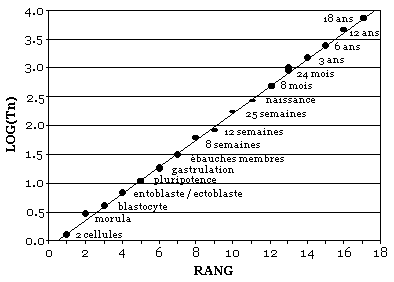
Figure 6. Logarithme décimal logTn des
dates des étapes du développement humain, comptées
à partir de la conception, en fonction de leur rang n . La
hauteur des points donne l'intervalle de confiance sur les dates (on a
supposé une barre d'erreur de +/-12 % sur les trois première
dates).
Plus récemment elle a été utilisée pour décrire la chronologie de l'embryogenèse et du développement humain [16] (Fig. 6).
5.2 D'une à plusieurs variables
d'échelle [18].
Ce cas correspond à la prise en considération de résolutions
différentes suivant les variables (spatiales et temporelles). Les
transformations correspondantes ne sont plus de simples dilatations globales,
mais prennent une forme multidimensionnelle plus compliquée (tensorielle).

Figure 7. Dépliage d'une surface fractale (deuxième
niveau d'itération).
5.3 De la relativité d'échelle
"galiléenne" à la relativité d'échelle restreinte
et généralisée [2,3].
On montre que les lois de transformation d'échelle de type fractale
auto-similaire (à dimension fractale constante) ont une structure
de groupe semblable à celle du groupe de Galilée en relativité
du mouvement. Ceci permet d'identifier ces lois standard à une relativité
"galiléenne" d'échelle. Mais ceci implique également,
comme dans le cas du mouvement, des généralisations possibles
à de nouvelles lois d'échelle, "Lorentziennes" [2], ou "Einsteiniennes".
5.4 De variables d'échelles
constantes à des variables d'échelle dépendantes des
coordonnées.
Le cas où on considère des résolutions spatio-temporelles qui peuvent elles-mêmes varier en fonction de la position et du temps (ce qui est un cas particulier de la relativité générale d'échelle évoquée ci-dessus) génère des champs d'origine purement géométrique [5]. Autrement dit, de même que le champ de gravitation s'identifie en relativité générale d'Einstein aux manifestations de la courbure, de même la fractalité va se manifester par l'apparition d'un ou de plusieurs champs.
Cette approche apporte une explication nouvelle à la nature des champs de jauge (interactions électromagnétiques, faibles et fortes), mais elle implique également la possibilité d'apparition de champs effectifs nouveaux (il s'agit d'énergie potentielle stockée dans la structure géométrique fractale elle-même) générés par les transformations d'échelle de matériaux structurés en échelle (Fig.7), i.e. fractals, donc en particulier les systèmes vivants. De nombreuses applications dans le domaine des sciences de la vie sont envisageables.
5.5 D'une description
classique déterministe à une description quantique dans l'espace
des échelles (description dans laquelle seules des
probabilités d'existence d'une structure à une échelle
relative donnée peuvent être définies).
Une telle mécanique quantique dans l'espace des échelles
génère des solutions qui décrivent (de manière
probabiliste) une ORGANISATION HIERARCHIQUE [18,19] (Fig.8).
Le nombre de niveaux hiérarchiques imbriqués les uns dans les autres est défini par une nouvelle quantité conservative (quantifiée dans ce cas) que j'ai nommée (pour cette raison) "complexergie" [18,19]. Des prédictions quantitatives sur les rapports d'échelles entre niveaux dans des conditions données sont envisageables.
Une telle approche est applicable aux toutes premières étapes
de l'évolution: passage de cellules sans noyau à un niveau
d'organisation principal, aux cellules eucayote présentant deux
niveaux d'organisation, puis aux multicellulaires formés de cellules
à noyaux montrant trois niveaux d'organisation imbriqués.
Elle rend compte ainsi du fait que les multicellulaires sont formés
d'eucaryotes et jamais de procaryotes.
La question de l'origine peut également être posée d'une manière renouvelée dans ce cadre: le premier niveau de hiérarchie apparait comme un état fondamental correspondant à la valeur minimale possible (non nulle) de la complexergie. Cet état résulte lui-même d'une structuration du milieu "extérieur", en dépendance des propriétés de ce même milieu (environnement), comme décrit par les champs, les conditions aux limites et les conditions de symétrie.
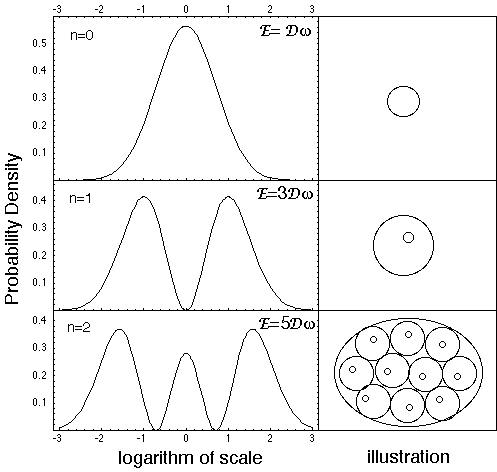
Figure 8. Solution de l'équation de Schrödinger
d'échelle (agissant dans l'espace des échelles) correspondant
à un potentiel d'oscillateur harmonique. Des systèmes de
"complexergie" croissante correspondent à un nombre croissant de
niveaux hiérarchiques imbriqués, comme observé dans
les premières étapes de l'évolution (procaryotes,
eucaryotes, multicellulaires).
6) Mécanique quantique généralisée
On étudie ensuite les effets induits par les structures internes en échelle sur le mouvement dans l'espace ordinaire (ou encore sur les structures de l'espace-temps), donc sur la dynamique. Le postulat fondamental à cette étape est que les trajectoires sont données par les géodésiques d'un tel espace-temps fractal (c'est-à-dire les lignes "les plus courtes" du point de vue de l'invariant de longueur).
Trois effets au minimum sont induits par la non-différentiabilité et la fractalité de l'espace sur la nature de ses géodésiques:
* elles sont en nombre infini, en raison de la perte d'information impliquée par la géométrie fractale, ce qui mène à une approche statistique non déterministe;
* chacune d'entre elle est une courbe fractale (de dimension fractale 2 dans le cas critique d'un processus sans corrélation ni anticorrélation);
* il y a un double champ de géodésiques, en raison de l'iiréversibilité locale qu'implique la non-différentiabilité.
Ces trois effets sont alors inclus et combinés dans la définition d'un opérateur de dérivation covariante (en analogie avec la méthode essentielle de la relativité générale). En terme de cet opérateur, l'équation des géodésiques prend la forme très simple d'une équation du mouvement libre, DV/dt=0. Après un changement de variables, cette équation se transforme et s'intègre sous forme d'une équation de Schrödinger généralisée. En d'autres termes, la mécanique dans un espace fractal et nondifférentiable devient de type quantique [3,5,8]
La mécanique quantique standard de la microphysique n'est qu'un cas particulier (fondé de manière exclusive sur la constante de Planck h) de cette nouvelle mécanique. Celle-ci dépend d'un nouveau paramètre pouvant prendre des valeurs beaucoup plus générales et qui peut être défini comme constante d'auto-organisation spécifique au système considéré. Ceci permet d'envisager l'existence de comportements macroscopiques quasi-quantiques, dans les cas où les trois conditions ci-dessus sont réunies, ce qui semble une hypothèse admissible pour de nombreux systèmes vivants.
En particulier, la condition principale pour obtenir un fonctionnement de type quantique et pas seulement une description probabiliste classsique est l'irréversibilité, qui est précisément une caractéristique essentielle du vivant.
6.1 Morphogenèse,
auto-organisation
Une telle théorie fonctionnant comme la mécanique quantique,
c'est-à-dire non pas en terme d'une description déterministe
et de conditions initiales sur des trajectoires individuelles, mais en
terme d'une densité de probabilité déduite d'une fonction
d'onde (qui vient décrire statistiquement le comportement global
d'un très grand nombre de trajectoires fractales irréversibles)
possède des capacités uniques à prendre en compte
les problèmes de structuration, de morphogenèse, de formation
et d'évolution. Il s'agit d'une théorie naturelle de l'auto-organisation
aux potentialités de développement très larges [3,12,14,18,19].
Figure 9. Solution d'une équation de Schrödinger
décrivant un processus de croissance à partir d'un centre
avec brisure de symétrie haut-bas et force constante vers le bas).
Les "pétales", "sépales" et "étamines" émergent
tous de la même solution, et sont tracés suivant les angles
de probabilité maximale.
C'est ainsi qu'on s'attend, dans son cadre, à voir apparaitre des morphologies comme matérialisation de zones de plus haute probabilité. Celles-ci sont contraintes par les conditions aux limites, les forces appliquées ainsi que les symétries du problème. Il en résulte une discrétisation des morphologies possibles, mises en correspondance avec la quantification des quantités conservatives qui les définissent [14,18,19].
Une application de cette approche a déjà pu être
faite à des morphologies de type floral, obtenues comme solutions
les plus probables d'un processus de croissance à partir d'un centre
(Fig.9).
Une proposition d'utilisation de cette méthode dans l'étude
en halieutique de la hiérarchie de structures présentée
par la distribution des poissons de haute mer (individu, banc, amas, population)
a également été proposée [12].
Il est également envisageable d'appliquer une telle théorie quantique à l'organisation des réseaux de neurones et à leur fonctionnement collectif. La proposition que des effets quantiques interviendraient dans le fonctionnement même du cerveau a été faite par R. Penrose et d'autres auteurs, mais il ne pouvait s'agir alors que de la mécanique quantique microscopique régie par la constante de Planck, ce qui a été depuis invalidé. Dans le cadre de la relativité d'échelle cette proposition peut être reprise, en terme d'une constante macroscopique résultant de l'auto-organisation du système. Les propriétés de non-localité, de cohérence, de non-séparabilité, ainsi que les méthodes de description en terme d'états et de leurs changements qui sont caractéristiques du domaine quantique pourraient alors être appliquées sans contradiction à de tels systèmes et à leur évolution.
Une autre application possible est la construction de modèles de duplication. La quantification des morphologies possibles a pour conséquence qu'une augmentation d'énergie ne conduira pas à une augmentation de taille du système, mais à un changement de sa structure. Dans le cas illustré Figure 10 (solutions d'une équation de Schrödinger dans un potentiel d'oscillateur harmonique tridimensionnel isotrope), étant donné que l'énergie est elle-même quantifiée, son augmentation ne permettra pas l'apparition d'une nouvelle structure avant qu'elle n'ait atteint son niveau de quantification suivant. Pour cette énergie c'est alors un système double qui apparait [18,19].
Si l'on suit les trajectoires fractales depuis le système
simple initial jusqu'au système double final, on trouve que tous
les points du système initial se retrouvent dans chacun des deux
sous-systèmes finaux.
Figure 10. Modèle de duplication. Quand l'énergie augmente d'un facteur 5/3, le système fondamental unique se divise en deux sous-systèmes.
Appliqué sur une coordonnée spatiale et non seulement
temporelle, un tel modèle pourra décrire des processus de
croissance avec bifurcation et branchement [18,19] (Fig.
11).
Figure 11. Modèle de croissance avec branchement (solution
bi-dimensionnelle dépendant du temps d'une équation de Schrödinger
dont l'énergie saute du niveau fondamental au premier niveau excité).
Les différents éléments de modélisation qui semblent émerger d'une telle approche théorique fondée sur le principe de relativité d'échelle (parois, hiérarchie d'organisation, morphogénèse, évolution, ...) peuvent être combinés entre eux dans le cadre d'une description théorique élaborée qui recombine elle-même les conditions sur lesquelles ces divers comportements sont fondés (effets induits dans l'espace-temps par des lois d'échelle non-linéaires, etc...).
Notons enfin pour finir ce bref résumé qu'un des domaines d'application privilégié d'une telle approche concerne la médecine: (modélisation du processus tumoral [20], etc...).
Références (ordre chronologique)
Sur la théorie de la relativité d'échelle:
[1] Nottale, L., 1989, International Journal of Modern Physics, A4,
5047-5117
"Fractals and the Quantum Theory of Space-Time".
[2] Nottale, L., 1992, International Journal of Modern Physics A7, 4899-4936
(PDF)
"The Theory of Scale Relativity".
[3] Nottale, L., 1993, (World Scientific, 1993), (LIVRE, 333 pp.)
"Fractal Space-Time and Microphysics: Towards a Theory of Scale Relativity."
[4] Nottale, L., 1995, Pour la Science, 215, 34 (Septembre 1995)
"L'Espace-Temps Fractal".
[5] Nottale, L., 1996, Chaos, Solitons and Fractals, 7, 877-938 (article
de revue) (PDF)
"Scale Relativity and Fractal Space-Time: Application to Quantum Physics,
Cosmology and Chaotic systems"
[6] Nottale, L., 1998, Hachette, collection "Sciences", (LIVRE, 319
pp), réédité dans la collection Pluriel (2000).
"La Relativité dans tous ses Etats : Au delà de l'Espace-Temps".
[7] Nottale, L., 2003, Pour La Science, 309, 38-45 (Juillet 2003)
"La relativité d'échelle à l'épreuve des
faits".
[8] Célérier M.N. & Nottale L., 2004, J. Phys. A,
37, 931 (PDF)
"Quantum-classical transition in scale relativity"
Impliquant le thème "relativité d'échelle et sciences de la vie":
[9] Nottale, L., 1997, in "Scale invariance and beyond", proceedings
of Les Houches school, Ed. B. Dubrulle, F. Graner and D. Sornette, (EDP
Sciences / Springer), p. 249 (PDF)
"Scale relativity"
[10] Chaline, J., Nottale, L., Grou, P., 1999, C.R. Acad. Sci. Paris,
328, IIa, 717 (PDF)
"L'arbre de la vie a-t-il une structure fractale ?".
Réimprimé dans: "Points sur... Sciences de la Terre IX:
évolution", (Académie des Sciences, Elsevier 2001)
http://www.daec.obspm.fr/users/nottale/arCNGcra.pdf
[11] Nottale, L., Chaline, J., & Grou, P., 2000, Hachette, 379 pp.
"Les arbres de l'évolution: Univers, Vie, Sociétés"
(LIVRE)
[12] Nottale, L., 2000, Conférence invitée, Proceedings
of 4è Forum Halieumétrique, Juin 1999, Les espaces de l'halieutique,
Eds. D. Gascuel, P. Chavance, N. Bez & A. Biseau, IRD Editions, p.41.
(PDF)
"La théorie de la relativité d'échelle: réflexions
pour une application à l'halieutique".
[13] Nottale, L., Chaline, J., & Grou, P., 2001, in "Fractals in
Biology and Medicine", Vol III, Proceedings of Fractal 2000 Third International
Symposium, Eds. G. Losa, D. Merlini, T. Nonnenmacher and E. Weibel, Birckhäuser
Verlag, p. 247. (PDF)
"On the fractal structure of evolutionary trees"
[14] Nottale L., 2001, Revue de Synthèse, T. 122, 4e S., Ndeg.1,
janvier-mars 2001, p. 93-116 (PDF)
"Relativité d'échelle et morphogenèse"
[15] Nottale L., 2002, in Traité IC2, Traitement du Signal et
de l'Image, "Lois d'échelle, fractales et ondelettes", sous la direction
de P. Abry, P. Gonçalvès et J. Levy Vehel (Hermès
Lavoisier 2002), Vol. 2, Chap. 7, pp. 233-265. (PDF)
"Relativité d'échelle, nondifférentiabilité
et espace-temps fractal"
[16] Cash R., Chaline, J., Nottale, L., Grou, P., 2002, C.R. Biologies
325, 585-590 (PDF)
"Développement humain et loi log-périodique".
[17] Grou P., Nottale L.,Chaline J., 2002, présenté dans
"Evénements rapides, instabilités, changements culturels
au quaternaire", Colloquium, Aix-en-Provence. Publié dans "En mémoire
de E. Aguirre", sous presse (PDF)
"Evolution morphologique et culturelle humaine: l'apport des modèles
fractals"
[18] Nottale L., 2003, (soumis, 76 pp., article de revue). (PDF)
"Fractal Space-Time, Nondifferentiable Geometry and Scale Relativity"
[19] Nottale L., 2004, contribution invitée in CASYS'03, Sixth
International Conference on Computing Anticipatory Systems (Liège,
Belgique, Aout 2003), AIP Conference Proceedings, à paraître
(PDF)
"The Theory of Scale Relativity: Non-Differentiable Geometry
and Fractal Space-Time"
[20] Pocard M., Rouleau E., Grou P., Nottale L., en préparation
(2004)