L. Nottale
Mis à jour le 30 Janvier 2006
L'information résumée dans ces pages a été publiée dans les références suivantes:
Astronomy and Astrophysics 315, L9 (1996) .
Astronomy and Astrophysics 322, 1018 (1997), avec G. Schumacher et J. Gay.
Astronomy and Astrophysics 361, 379 (2000), avec G. Schumacher et E.T. Lefèvre.
La théorie de relativité d'échelle permet de poser d'une manière nouvelle le problème de la formation et de l'évolution des systèmes planétaires.
Comme dans le modèle standard de formation, les planètes sont supposées être formées par accrétion de planétésimaux. Toutefois, la distribution initiale de la densité de probabilité de ces planétésimaux ne peut plus être quelconque dans la nouvelle théorie, mais au lieu de cela est donnée par les solutions d'une équation de Schrödinger généralisée.
Une telle équation de type Schrödinger est obtenue à partir d'une généralisation de l'équation de la dynamique de Newton dans laquelle des termes de fluctuation et d'irréversibilité ont été inclus : ceux-ci sont destinés à décrire les structures fractales internes de l'espace-temps. Ces structures ne se révèleraient, dans ce domaine, qu'aux grandes échelles temporelles (grandes relativement à une échelle temporelle de transition au delà de laquelle l'information sur les orbites individuelles est perdue, quelle qu'en soit la raison: chaos, diffusion, collisions, perturbations diverses, micro-structures de l'espace...).
Les solutions de l'équation de la dynamique ainsi généralisée définissent, dans le cas d'un potentiel de Kepler (problème à deux corps), des "orbitales" similaires à celles de l'atome d'hydrogène.
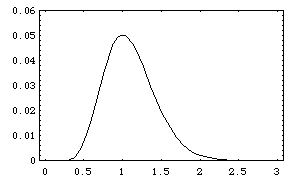
Exemple de distribution de densité de probabilité (n = 5):

On s'attend à ce que les planétésimaux remplissent de telles orbitales, puis forment une planète par accrétion. La valeur finale du demi-grand axe de la planète est donnée au premier ordre par le pic de probabilité de l'orbitale. Les positions de ces pics ne peuvent prendre que les valeurs quantifiées données par :
an = GM n2 / w2.
Dans cette formule, M est la masse de l'étoile centrale et w est une constante ayant la dimension d'une vitesse. On s'attend à ce que la théorie s'applique à des systèmes gravitationnels à deux corps quelle que soit l'échelle, c.à.d., pas seulement à des configurations étoile-planète, mais aussi aux étoiles doubles et aux paires de galaxies (effet Tifft). A partir de plusieurs échantillons galactiques et extragalactiques, on trouve que cette constante w est un multiple ou un sous-multiple (suivant le système particulier considéré) de la constante universelle:
w0 = 144.7 ± 0.6 km/s .
Il est facile de vérifier que notre Système Solaire interne
est structuré en accord avec cette loi et que les planètes
extra-solaires récemment découvertes s'accordent également
remarquablement bien avec elle. Il faut insister sur le fait que ce n'est
pas une loi de type Titius-Bode (elle n'est pas invariante-d'échelle),
et surtout que cette loi est totalement contrainte: il n'y a aucun ajustement
dans
les figures ci-dessous.
Comparaison entre les positions observées des planètes autour d'étoiles de type solaire et les distances prédites des pics de densité de probabilité (1996):
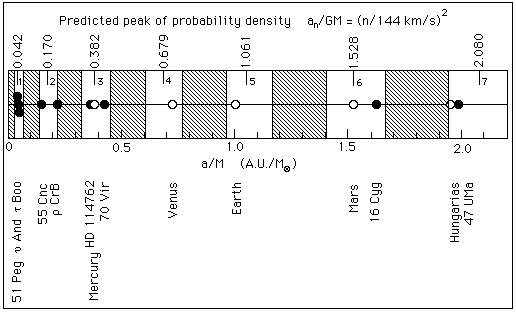
Pour les planètes extra-solaires (voir catalogue), les rapports a/M sont calculés à partir des périodes (dérivées du mouvement réflexe observé de l'étoile) en utilisant la troisième loi de Kepler. Leur incertitude est dominée par l'incertitude sur la masse de l'étoile, (10% dans la plupart des cas), que nous avons estimée à partir de son type spectral quand aucune détermination plus précise n'existe. Les bandes blanches correspondent aux zones de hautes probabilité, c.-à.-d. à des n effectifs dans l'intervalle [n-1/4, n+1/4]. Les bandes grises sont les zones de basse probabilité, c.-à.-d. des n effectifs dans l'intervalle [n+1/4, n+3/4]. Les n effectifs sont donnés, en fonction de la période observée T en jours et de la masse M de l'étoile en masse solaire, par (T / 3.25 M)1/3. La figure exprime qu'ils se regroupent autour de valeurs entières.
La probabilité d'obtenir une telle configuration par hasard est P = 2-14 = 6 10^-5.
Une des plus étonnantes prédictions de la théorie, qui a été effectuée "en aveugle" quatre ans avant les premières découvertes de planètes extra-solaires (reprise par exemple dans L. Nottale, Fractal Space-Time and Microphysics, WorldScientific, 1993, Chapitre 7.2) est que le pic de l'orbitale fondamentale n = 1 se trouve autour de 0.043 U.A. pour les étoiles de 1 masse solaire. La découverte de 51 Peg B, puis de deux planètes supplémentaires précisément à cette distance de leur étoile a apporté une confirmation remarquable de cette prédiction (1996). Quatre ans plus tard, ces premiers résultats restent confirmés: ce sont maintenant 9 planètes et 2 naines brunes qui se concentrent autour de cette valeur (Oct. 2000). La figure suivante donne l'état actuel de la distribution des demi-grands axes des 50 exoplanètes connues à ce jour. La probabilité d'obtenir par hasard une telle concentration autour des pics de densité prédits est de 1/10000.
Comparaison entre les demi-grands-axes observés des planètes autour d'étoiles de type solaire et les pics de densité de probabilité prédits (Octobre 2000): on s'attend à ce que les valeurs de la variable 4.83(a/M)1/2 , c'est-à-dire d'une manière équivalente (d'après la troisième loi de Kepler), 4.83(T/M)1/3 = (w0/v), se concentrent autour de nombres entiers.
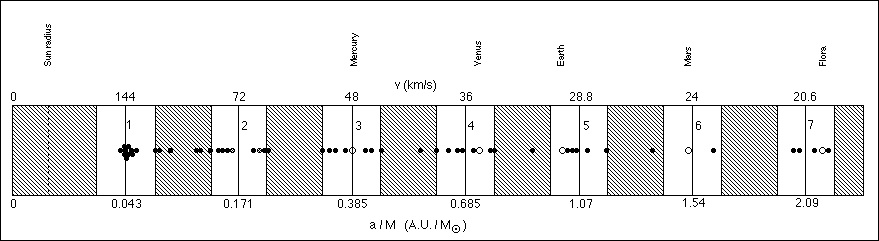
Distribution des demi-grands axes des exoplanètes (Juin 2005)
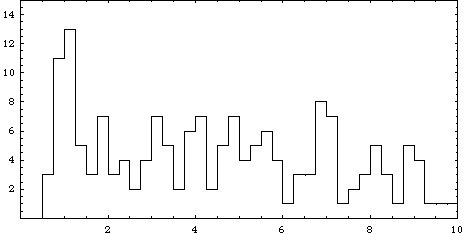
Distribution observée de la varable n = 4.83(a/M)1/2
=
4.83(T/M)1/3
Mercure, Vénus, la Terre et Mars
sont respectivement dans les pics n=3,4,5 et 6
Comparaison entre les périodes observées et prédites des planètes du pulsar PSR B1257+12
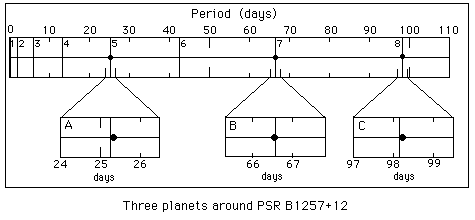
Dans le cas du système planétaire qui entoure le pulsar
PSR
B1257+12 (Wolszczan, 1994, Science 264, 538), l'accord
entre théorie et observations est si bon que les termes d'ordre
supérieur peuvent être éprouvés. La distance
moyenne
de la distribution de densité de probabilité est quantifiée
comme n2 +n/2. En utilisant la troisième loi de Kepler,
on trouve que l'on peut prédire les périodes de deux des
planètes à partir de la troisième avec une incertitude
de l'ordre de l'heure (alors que les périodes sont de 1 à
3 mois, voir figure). La probabilité d'obtenir un tel résultat
par hasard est seulement P < 10?4. Si
d'autres planètes existent dans ce système, leurs périodes
attendues (dans le cas où elles sont inférieures à
200 jours) sont les suivantes:
| 0.322 | 1.957 | 5.956 | 13.37 | 25.24 | 42.63 | 66.58 | 98.15 | 138.4 | 188.3 |
| 25.34 | 66.54 | 98.22 |
Cette table donne les périodes prédites (en jours) pour
n = 1 à 10, et les compare aux trois périodes observées
(Wolszczan A., 1994). Remarquer que les fluctuations de ces périodes
orbitales dues aux perturbations gravitationnelles mutuelles ont été
observées et sont de l'ordre de 0.02 jours.
Complément d'information:
Références:
L. Nottale, Fractal Space-Time and Microphysics (World Scientific, 1993), Chapitre 7.2, pp. 307-321: "Beyond chaos" (PDF)
L. Nottale, in "Cellular Automata, Prospects in Astrophysical Applications", Eds. J.M. Perdang & A. Lejeune, Proceedings of Han-sur-Lesse Colloquium, Octobre 1992 (World Scientific, 1993), p. 268: "Emergence of structures from chaos"
L. Nottale, 1995, invited conference in "Chaos and diffusion in Hamiltonian systems", (Chamonix, Février 1994), Ed. D. Benest et C. Froeschlé (Frontière), pp. 173-198. (PDF) "New Formulation of Stochastic Mechanics. Application to Chaos".
L. Nottale, 1996, Astron. Astrophys. Lett. 315, L9: "Scale relativity and quantization of extra-solar planetary systems"
L. Nottale, G. Schumacher & J. Gay, 1997, Astron. Astrophys.322,1018: "Scale relativity and quantization of the Solar System"
L. Nottale, 1998, Chaos, Solitons & Fractals, 9, 1043: "Scale relativity and quantization of the planetary system around the pulsar PSR B1257+12"
L. Nottale, G. Schumacher & E.T. Lefèvre, 2000, Astron. Astrophys. 361, 379: "Scale relativity and quantization of exoplanet orbital semi-major axes"
Da Rocha D. & Nottale L., 2003, Chaos Solitons and Fractals, 16, 565 (PDF) (arXiv:astro-ph/0310036) "Gravitational structure formation in scale relativity"
L. Nottale, D. Ceccolini, D. DaRocha, N. Tran-Minh, P. Galopeau, G. Schumacher, 2003, in "Extrasolar Planets: Today and Tomorrow", Proceedings of IAP meeting, Paris, 30 juin-4 Juillet 2003, Eds. J.P. Beaulieu, A. Lecavelier des Etangs and C. Terquem, Astronomical Society of the Pacific Conference Series vol. 321, p. 355 (PDF) (JPEG) "Structuring of the semi-major axis and eccentricity distributions of exoplanets"
P. Galopeau, L. Nottale, D. Ceccolini, D. DaRocha,
G. Schumacher and N. Tran-Minh, 2004, in "Scientific
Highlights 2004", Proceedings of the Journées
de la SF2A, Paris 14-18 Juin 2004, F. Combes, D. Barret,
T. Contini, F. Meynadier & L. Pagani (eds.), EDP Sciences, p. 75 (Poster
présenté aux Journées de la
SF2A) (JPEG)
"Distribution of orbital elements of planets and exoplanets in scale relativity"