L. Nottale
Updated 30 January 2006
The information summarized in these pages has been published in the following references:
Astronomy and Astrophysics 315, L9 (1996) .
Astronomy and Astrophysics 322, 1018 (1997), with G. Schumacher et J. Gay.
Astronomy and Astrophysics 361, 379 (2000), with G. Schumacher et E.T. Lefèvre.
Astronomy and Astrophysics (2001), submitted, with N. Tran Minh
The theory of scale relativity allows one to set in a renewed way the problem of the formation and evolution of planetary systems.
As in the standard model of formation, the planets are assumed to be formed by accretion of planetesimals. However, the initial distribution of probability density of these planetesimals can no longer be any distribution in our theory, but is instead given by the solutions of a generalized Schrödinger equation.
Such a Schrödinger-like equation is obtained from a generalization of Newton's equation of dynamics in which fluctuation and irreversibility terms aimed at describing the assumed inner fractal structures of space-time have been included. These structures show up, in this domain, only at long time scales (namely, long relatively to some transition time-scale, beyond which the information about the individual orbits is lost, whatever the cause: chaos, diffusion, collisions, various perturbations, micro-structure of space...).
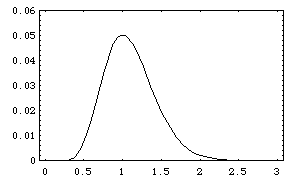
The solutions of the equation of dynamics generalized in this way define, in the case of a Kepler potential (two-body problem), "orbitals" similar to that of the hydrogen atom.
Example of probability density distribution (n = 5):

The planetesimals are expected to fill such orbitals, then to form a planet by accretion. The final value of the semi-major axis of the planet orbit is given to lowest order by the probability peak of the orbital. The positions of these peaks can take only quantized values given by :
an = GM n2 / w2.
In this formula (which corresponds to circular orbits), M is the mass of the central star and w is a constant having the dimension of a velocity. The theory is expected to apply to two-body gravitational systems whatever the scale, i.e., not only to star-planet configurations, but also double stars and binary galaxies (Tifft effect). From several galactic and extragalactic samples, this constant is found to be a multiple or submultiple (depending of the particular system considered) of the universal constant:
w0 = 144.7 ± 0.6 km/s .
It is easy to verify that our own inner Solar System is structured according
to this law and that the recently discovered extra-solar planets also agree
remarkably well with it. We stress the fact that this is not a Titius-Bode-like
law (it is not scale-invariant), and mainly that this law is totally constrained:
there is no fit in the figures below.
Comparison between the observed positions of planets around solar-type stars and the predicted distances of probability density peaks (1996):
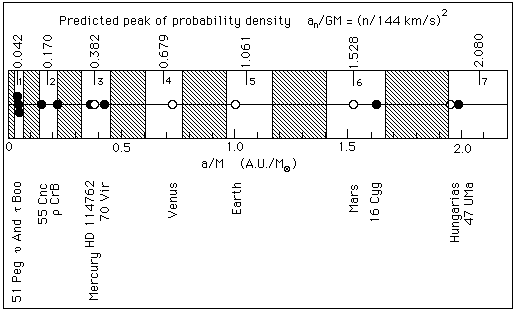
For extra-solar planets (see catalog), the ratios a/M are computed from the periods (derived from the observed reflex motion of the star) using Kepler's third law. Their uncertainty is dominated by the uncertainty on the star mass, (10% in most cases), which we have derived from its spectral type when no more precise determination exists. The white bands correspond to the high probability zones, i.e. to effective n's in the interval [n-1/4, n+1/4]. The grey bands are for low probability zones, i.e. effective n's in the interval [n+1/4, n+3/4]. The effective n's are given, in terms of the observed period T and of the estimated star mass M, by (T / 3.25 M)1/3. The figure shows their clustering around integer values.
The probability to obtain such a configuration by chance is P = 2?14 = 6 10?5.
One of the most remarkable predictions of the theory, which has been performed "in a blind way" four years before the first discovery of extra-solar planets, is that the peak of the fundamental orbital n = 1 lies around 0.043U.A. for 1 solar mass stars. The discovery of 51 Peg B, then of two additional planets at such a distance from their star has been a remarkable confirmation of that prediction (1996).
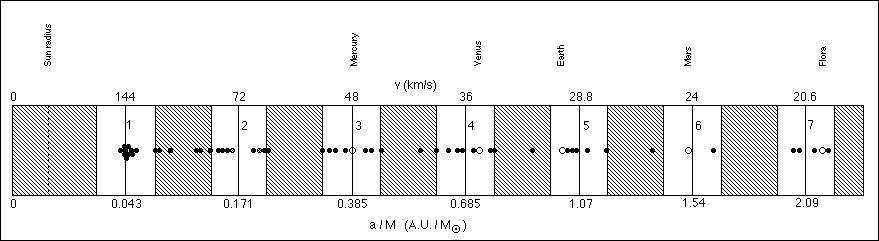
Four years later, these first results remain supported by more recent observations: there are now 9 planets and 2 brown dwarfs concentrated around this value (Oct. 2000). The average velocity of these 11 objects is 142.6 ± 2.5 km/s, which includes within error bars the expected value 144. 7 km/s. The following figure gives the present state of the distribution of semi-major axes of the 50 exoplanets now known. The probability to obtain such a concentration around the predicted density peaks is 1/10000.
Comparison between the observed semimajor axes of planets around solar-type stars and the predicted probability density peaks (2000): we expect the variable 4.83(a/M)1/2 , i.e. equivalently (from Kepler's third law), 4.83(T/M)1/3 = (w0/v), to cluster around integer values.
Distribution of exoplanet semimajor axes (June 2005)
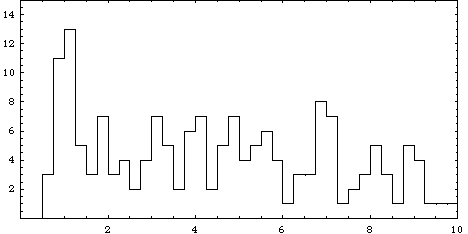
Observec distribution of the varable n = 4.83(a/M)1/2
=
4.83(T/M)1/3
Mercury, Venus, the Earth and Mars lie
respectively in the peaks n=3,4,5 and 6
Comparison between the observed and predicted periods of planets around the pulsar PSR B1257+12
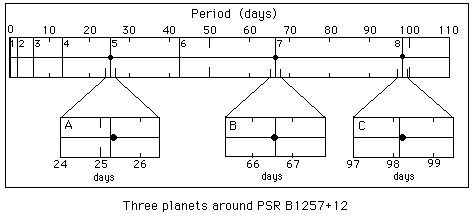
In the case of the planetary system around the pulsar PSR
B1257+12 (Wolszczan, 1994, Science 264, 538), the agreement
between theory and observations is so good that higher order terms can
be tested. The mean distance of the probability density distribution
is quantized as n2 +n/2. Using Kepler's third law, we find that
we can predict the periods of two of the planets from the third with an
uncertainty of about 1 hour (see figure). The probability of obtaining
such a result by chance is only P < 10?4.
If other planets exist in this system, their expected periods (in the case
when they are smaller than 200 days) are as follows:
| 0.322 | 1.957 | 5.956 | 13.37 | 25.24 | 42.63 | 66.58 | 98.15 | 138.4 | 188.3 |
| 25.34 | 66.54 | 98.22 |
The table gives the predicted periods (in days) for n = 1 to 10, and compares them to the three observed periods (Wolszczan A., 1994). Remark that the fluctuations of these orbital periods due to mutual gravitational perturbations have been observed and are of the order of 0.02 days.
Additional informations:
References:
L. Nottale, Fractal Space-Time and Microphysics (World Scientific, 1993), Chapter 7.2, pp. 307-321: "Beyond chaos" (PDF)
L. Nottale, in "Cellular Automata, Prospects in Astrophysical Applications", Eds. J.M. Perdang & A. Lejeune, Proceedings of Han-sur-Lesse Colloquium, Oct. 1992 (World Scientific, 1993), p.268: "Emergence of structures from chaos"
L. Nottale, 1995, invited conference in "Chaos and diffusion in Hamiltonian systems", (Chamonix, Février 1994), Ed. D. Benest et C. Froeschlé (Frontière), pp. 173-198. (PDF) "New Formulation of Stochastic Mechanics. Application to Chaos".
L. Nottale, 1996, Astron. Astrophys. Lett. 315, L9 : "Scale relativity and quantization of extra-solar planetary systems"
L. Nottale, G. Schumacher & J. Gay, 1997, Astron. Astrophys. 322, 1018: "Scale relativity and quantization of the Solar System"
L. Nottale, 1997, Chaos, Solitons & Fractals, 9, 1043: "Scale relativity and quantization of the planetary system around the pulsar PSR B1257+12"
L. Nottale, G. Schumacher & E.T. Lefèvre, 2000, Astron. Astrophys. 361, 379: "Scale relativity and quantization of exoplanet orbital semi-major axes"
Da Rocha D. & Nottale L., 2003, Chaos Solitons and Fractals, 16, 565 (PDF) (arXiv:astro-ph/0310036) "Gravitational structure formation in scale relativity"
L. Nottale, D. Ceccolini, D. DaRocha, N. Tran-Minh, P. Galopeau, G. Schumacher, 2003, in "Extrasolar Planets: Today and Tomorrow", Proceedings of IAP meeting, Paris, 30 juin-4 Juillet 2003, Eds. J.P. Beaulieu, A. Lecavelier des Etangs and C. Terquem, Astronomical Society of the Pacific Conference Series vol. 321, p. 355 (PDF) (JPEG) "Structuring of the semi-major axis and eccentricity distributions of exoplanets"
P. Galopeau, L. Nottale, D. Ceccolini, D. DaRocha,
G. Schumacher and N. Tran-Minh, 2004, in "Scientific
Highlights 2004", Proceedings of the Journées
de la SF2A, Paris 14-18 Juin 2004, F. Combes, D. Barret,
T. Contini, F. Meynadier & L. Pagani (eds.), EDP Sciences, p. 75 (Poster
présenté aux Journées de la
SF2A) (JPEG)
"Distribution of orbital elements of planets and exoplanets in scale relativity"